题目内容
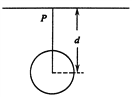
【题目】某地区的地下发现天然气资源，如图所示，在水平地面P点的正下方有一球形空腔区域内储藏有天然气．假设该地区岩石均匀分布且密度为ρ，天然气的密度远小于ρ，可忽略不计．如果没有该空腔，地球表面正常的重力加速度大小为g；由于空腔的存在，现测得P点处的重力加速度大小为kg (其中k<l)．已知引力常量为G，球形空腔的球心深度为d，则此球形空腔的体积是
A. 
B. 
C. 
D. 
【答案】C
【解析】如果将近地表的球形空腔填满密度为ρ的岩石，则该地区重力加速度便回到正常值，因此，如果将空腔填满，地面质量为m的物体的重力为mg，没有填满时是kmg，故空腔填满后引起的引力为（1-k）mg；根据万有引力定律，有： 
, 解得： 
故选C.
练习册系列答案
相关题目
