题目内容
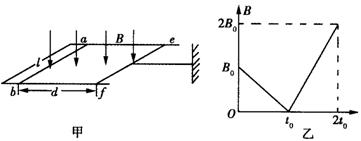
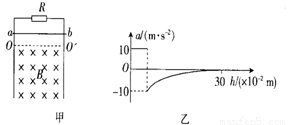
如图甲所示，电阻不计且间距L=lm的光滑平行金属导轨竖直放置，上端接一阻值R=2Ω的电阻，虚线OO′下方有垂直于导轨平面向里的匀强磁场，现将质量m=0.l kg、电阻不计的金属杆ab从OO′上方某处由静止释放，金属杆在下落的过程中与导轨保持良好接触且始终水平。已知杆ab进入磁场时的速度v0 =1m/s，下落0.3 m的过程中加速度a与下落距离h的关系图象如图乙所示，g取10 m/s2 ，则
A．匀强磁场的磁感应强度为1T
B．ab杆下落0.3 m时金属杆的速度为1 m/s
C．ab杆下落0.3 m的过程中R上产生的热量为0.2 J
D．ab杆下落0.3 m的过程中通过R的电荷量为0.25 C
【答案】
D
【解析】
试题分析：金属杆刚进入磁场时，速度为v0 =1m/s，据图此时的加速度为a=-10m/s2，经受力分析此时有：mg-BIL=-ma，I=BLv/R,则磁感应强度为B=2T，A选项错误；金属杆下落h=0.3m时，据图可知此时加速度a=0，所以此时有mg=BIL，I=BLv‘/R则v‘=0.5m/s，所以B选项错误；金属杆下落0.3m的过程中R产生的热量为mgh-Q=mv’2/2-mv02/2，则Q=0.3375J，所以C选项错误；金属杆下落h=0.3m过程中产生的电荷量为q=It=BS/R=BLh’/R，h’=h-v02/2g,所以q=0.25C，则D选项正确。
考点：本题考查电磁感应，牛顿第二定律，平衡条件，能量守恒定律和运动学关系的应用。
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
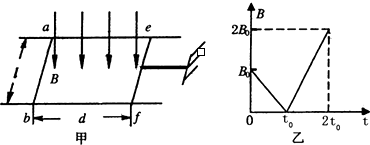如图甲所示，电阻不计，间距为l的平行长金属导轨置于水平面内，阻值为R的导体棒ab固定连接在导轨左端，另一阻值也为R的导体棒ef垂直放置到导轨上，ef与导轨接触良好，并可在导轨上无摩擦移动．现有一根轻杆一端固定在ef中点，另一端固定于墙上，轻杆与导轨保持平行，ef、ab两棒间距为d．若整个装置处于方向竖直向下的匀强磁场中，且从某一时刻开始，磁感应强度B随时间t按图乙所示的方式变化．
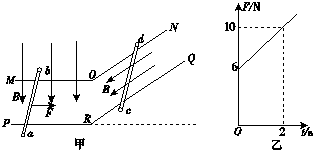如图甲所示，电阻不计的轨道MON与PRQ平行放置，ON及RQ与水平面的夹角θ=53°，水平导轨处于竖直向下的匀强磁场中，倾斜导轨处于平行轨道向下的磁场中，磁场的磁感应强度大小相同．两根相同的导体棒ab和cd分别放置在导轨上，与导轨垂直并始终接触良好．导体棒的质量m=1.0kg，R=1.0Ω，长度L=1.0m，与导轨间距相同，两导体棒与导轨间的动摩擦因数μ=0.5．现对ab棒施加一个方向向右、大小随乙图规律变化的力F的作用，同时由静止释放cd棒，则ab棒做初速度为零的匀加速直线运动，g取10m/s2．求：（设解题涉及过程中ab、cd两棒分别位于水平和倾斜轨道上）