题目内容
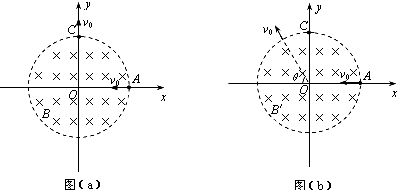
(2010?长沙县模拟)如图(a)所示,在以直角坐标系xOy的坐标原点O为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直xOy所在平面的匀强磁场.一带电粒子由磁场边界与x轴的交点A处,以速度v0沿x轴负方向射入磁场,粒子恰好能从磁场边界与y轴的交点C处,沿y轴正方向飞出磁场,不计带电粒子所受重力.
(1)求粒子的荷质比
.(要求画出粒子在磁场中运动轨迹的示意图)
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B′,该粒子仍从A处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b)所示,求磁感应强度B′的大小.(要求画出粒子在磁场中运动轨迹的示意图)
(1)求粒子的荷质比
| q | m |
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B′,该粒子仍从A处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b)所示,求磁感应强度B′的大小.(要求画出粒子在磁场中运动轨迹的示意图)

分析:(1)由洛伦兹力提供向心力,使其做匀速圆周运动,根据牛顿第二定律及几何关系,即可求解;
(2)当磁场变化时,粒子仍做匀速圆周运动,并由几何关系可求出结果.
(2)当磁场变化时,粒子仍做匀速圆周运动,并由几何关系可求出结果.
解答:解析:(1)由几何关系可知,粒子的运动轨迹如图1,
洛伦兹力等于向心力,即图两份
qv0B=m
因R=r
得
=
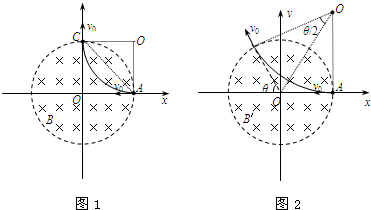
(2)粒子的运动轨迹如图2,设其半径为R′,洛伦兹力提供向心力,即
qv0B′=m
又因为 tan
=
解得 B′=Btan
答:(1)求粒子的荷质比为
.如图所示;
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B′,该粒子仍从A处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b)所示,则应强度B′的大小为Btan
.
洛伦兹力等于向心力,即图两份
qv0B=m
| ||
| R |
因R=r
得
| q |
| m |
| v0 |
| Br |

(2)粒子的运动轨迹如图2,设其半径为R′,洛伦兹力提供向心力,即
qv0B′=m
| ||
| R′ |
又因为 tan
| θ |
| 2 |
| r |
| R′ |
解得 B′=Btan
| θ |
| 2 |
答:(1)求粒子的荷质比为
| v0 |
| Br |
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B′,该粒子仍从A处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b)所示,则应强度B′的大小为Btan
| θ |
| 2 |
点评:考查带电粒子在洛伦兹力作用下,做匀速圆周运动,并由牛顿第二定律与几何关系相综合解题,注意运动轨迹的半径与圆形磁场半径的区别.

练习册系列答案
相关题目
 (2010?长沙县模拟)如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的a处有一粒子源,盒内粒子以v0=2.0×102m/s的初速度向水平面以下的各个方向均匀释放质量为m=2.0×10-15kg,电荷量为q=+10-12C的带电粒子,粒子最终落在金属板b上.若不计粒子重力,求:(结果保留两位有效数字)dysz
(2010?长沙县模拟)如图所示,某空间有一竖直向下的匀强电场,电场强度E=1.0×102V/m,一块足够大的接地金属板水平放置在匀强电场中,在金属板的正上方高度h=0.80m的a处有一粒子源,盒内粒子以v0=2.0×102m/s的初速度向水平面以下的各个方向均匀释放质量为m=2.0×10-15kg,电荷量为q=+10-12C的带电粒子,粒子最终落在金属板b上.若不计粒子重力,求:(结果保留两位有效数字)dysz
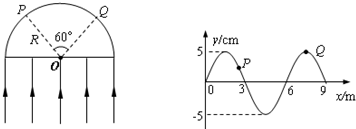 (3)一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y运动,经过0.1s第一次到达平衡位置,波速为5m/s,那么:
(3)一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y运动,经过0.1s第一次到达平衡位置,波速为5m/s,那么: