题目内容
18.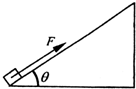 如图所示,已知一足够长粗糙斜面倾角为θ=37°,一质量m=15kg物体,在斜面底部受到一个沿斜面向上的F=300N的力作用由静止开始运动,物体在2秒内位移为20m,2秒末撤销力F,求:(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,已知一足够长粗糙斜面倾角为θ=37°,一质量m=15kg物体,在斜面底部受到一个沿斜面向上的F=300N的力作用由静止开始运动,物体在2秒内位移为20m,2秒末撤销力F,求:(sin37°=0.6,cos37°=0.8,g=10m/s2)(1)物体与斜面间的动摩擦因数?
(2)从撤销力F开始2秒末物体的速度?
分析 (1)物体先沿斜面向上做匀加速运动,撤去F后做匀减速运动.根据运动学公式求出前2s内物体的加速度,由牛顿第二定律和摩擦力公式求出物体与斜面间的动摩擦因数μ;
(2)由牛顿第二定律求出撤去F后物体的加速度,由速度公式求出撤去F开始2s末物体的速度v.
解答 解:(1)设力F作用时物体的加速度为a1,t1=2s,
由:s=$\frac{1}{2}$a1t12得:a1=$\frac{2s}{{t}_{1}^{2}}$=$\frac{2×20}{{2}^{2}}$=10m/s2,
有力F作用时,由牛顿第二定律得:
F-mgsinθ-μmgcosθ=ma1,解得:μ=0.5;
(2)设撤销力F的瞬间物体的速度为v1,则v1=a1t1=20m/s
设撤销力F以后,物体沿斜面减速上滑的加速度为a2,依牛顿第二定律有:
mgsinθ+μmgcosθ=ma2,解得:a2=10m/s2
撤销力F后物体做匀减速直线运动,速度减为零需要的时间:t2=$\frac{{v}_{1}}{{a}_{2}}$=$\frac{20}{10}$=2s,
故撤销力F后2s末物体的速度为:v=0m/s;
答:(1)物体与斜面间的动摩擦因数μ为0.5;
(2)从撤销力F开始2秒末物体的速度v为0m/s.
点评 本题运用牛顿第二定律和运动学公式结合求解动力学问题,要学会分析过程,把握住各个过程之间的联系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.如图所示电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是( )


| A. | 电流表读数变大,电压表读数变小 | B. | 小灯泡L变暗 | ||
| C. | 电容器C上电荷量减小 | D. | 电源的总功率变大 |
13.关于重力的说法正确的是( )
| A. | 重心一定是物体的几何中心 | |
| B. | 重力的方向是竖直向下的,一定指向地心 | |
| C. | 重心一定是物体上最重的一点 | |
| D. | 同一个物体在地球上纬度不同的地方所受重力不相同 |
10.关于参考系的说法中错误的是( )
| A. | 研究物体的运动时,首先要先选定好参考系 | |
| B. | 描述一个物体的运动时,参考系可以任意选择,但选择不同的参考系,观察同一个物体的运动,其结果会有所不同 | |
| C. | 我们常说物体处于静止状态,其实是相对于其他物体而言的,这便是运动的相对性 | |
| D. | 只有静止的物体才能被选作参考系 |
 一质量为m=2×103kg的小轿车,驶过半径R=80m的一段圆弧形桥面,重力加速度g取10m/s2,求:
一质量为m=2×103kg的小轿车,驶过半径R=80m的一段圆弧形桥面,重力加速度g取10m/s2,求: 如图所示,在场强E=104 N/C的水平匀强电场中,有一根长L=15cm的细线,一端固定在O点,另一端系一个质量m=3g,带电荷量q=2×10-6 C的小球,当细线处于水平位置时,小球从静止开始释放,则
如图所示,在场强E=104 N/C的水平匀强电场中,有一根长L=15cm的细线,一端固定在O点,另一端系一个质量m=3g,带电荷量q=2×10-6 C的小球,当细线处于水平位置时,小球从静止开始释放,则 如图所示,电阻R1=8Ω,电动机绕组电阻R0=2Ω,当开关S断开时,电阻R1消耗的电功率是2.88W;当开关S闭合时,电阻R1消耗的电功率是2W.若电源的电动势为6V,求开关S闭合时
如图所示,电阻R1=8Ω,电动机绕组电阻R0=2Ω,当开关S断开时,电阻R1消耗的电功率是2.88W;当开关S闭合时,电阻R1消耗的电功率是2W.若电源的电动势为6V,求开关S闭合时 如图所示,两块正对的带电金属板,上板的电势高于下板,板间的电场强度为200N/C,两板之间的距离为0.2m,板长为0.4m,带电粒子以5×104m/s的速度从极板左端垂直于电场方向进入电场,从极板右端飞出,虚线为粒子的运动轨迹,不计带电粒子所受重力,试问:
如图所示,两块正对的带电金属板,上板的电势高于下板,板间的电场强度为200N/C,两板之间的距离为0.2m,板长为0.4m,带电粒子以5×104m/s的速度从极板左端垂直于电场方向进入电场,从极板右端飞出,虚线为粒子的运动轨迹,不计带电粒子所受重力,试问: