题目内容
3. 如图所示,两块正对的带电金属板,上板的电势高于下板,板间的电场强度为200N/C,两板之间的距离为0.2m,板长为0.4m,带电粒子以5×104m/s的速度从极板左端垂直于电场方向进入电场,从极板右端飞出,虚线为粒子的运动轨迹,不计带电粒子所受重力,试问:
如图所示,两块正对的带电金属板,上板的电势高于下板,板间的电场强度为200N/C,两板之间的距离为0.2m,板长为0.4m,带电粒子以5×104m/s的速度从极板左端垂直于电场方向进入电场,从极板右端飞出,虚线为粒子的运动轨迹,不计带电粒子所受重力,试问:(1)带电粒子带何种电荷?
(2)两板间的电势差多大?
(3)带电粒子在电场中的运动时间多长?
(4)带电粒子的加速度的大小是多少?
(5)带电粒子的偏转距离是多少?
(6)带电粒子飞出电场的速度大小是多少?
分析 (1)两块正对的带电金属板,上板的电势高于下板,板间场强方向向下,根据粒子轨迹的偏转方向,判断电场力方向,即可知道粒子的电性.
(2)板间是匀强电场,由U=Ed求两板间的电势差.
(3)带电粒子在电场中做类平抛运动,平行于的方向做匀速直线运动,由t=$\frac{L}{{v}_{0}}$求时间.
(4)根据$\frac{1}{2}a{t}^{2}$=d求加速度.
(5)由y=$\frac{1}{2}a{t}^{2}$求偏转距离.
(6)由vy=at,v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$求解带电粒子飞出电场的速度或根据动能定理求.
解答 解:(1)两块正对的带电金属板,上板的电势高于下板,则板间场强方向向下,由图粒子向下偏转,说明受到的电场力方向竖直向下,故知该带电粒子带正电.
(2)因两板间是匀强电场,则两板间的电势差 U=Ed=200×0.2V=40V
(3)带电粒子在电场中做类平抛运动,平行于的方向做匀速直线运动,则运动时间为
t=$\frac{L}{{v}_{0}}$=$\frac{0.4}{5×1{0}^{4}}$s=8×10-6s
(4)根据y=d=$\frac{1}{2}a{t}^{2}$得:
带电粒子的加速度的大小是 a=$\frac{2d}{{t}^{2}}$=$\frac{2×0.2}{(8×1{0}^{-6})^{2}}$=6.25×109m/s2;
(5)带电粒子的偏转距离是y=d=0.2m
(6)根据动能定理得:
mad=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得 v=$\sqrt{{v}_{0}^{2}+2ad}$=$\sqrt{(5×1{0}^{4})^{2}+2×6.25×1{0}^{9}×0.2}$m/s=5$\sqrt{2}$×104m/s
答:
(1)带电粒子带正电.
(2)两板间的电势差为40V.
(3)带电粒子在电场中运动的时间为8×10-6s.
(4)带电粒子的加速度的大小是6.25×109m/s2.
(5)带电粒子的偏转距离是0.2m.
(6)带电粒子飞出电场的速度大小是5$\sqrt{2}$×104m/s.
点评 本题掌握公式U=Ed、能运用运动的分解处理带电粒子类平抛运动,结合力学的基本规律处理.

 如图,套在固定杆上的重物M沿竖直杆下滑,M通过绳带动小车水平向右运动,当定滑轮右侧的绳与水平方向的夹角为θ时M下滑的速率为v,此时小车的速率为( )
如图,套在固定杆上的重物M沿竖直杆下滑,M通过绳带动小车水平向右运动,当定滑轮右侧的绳与水平方向的夹角为θ时M下滑的速率为v,此时小车的速率为( )| A. | vsinθ | B. | vcosθ | C. | $\frac{v}{sinθ}$ | D. | $\frac{v}{cosθ}$ |
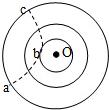 一带电粒子射入固定在O点的点电荷产生的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面,不计重力,下列判断正确的是( )
一带电粒子射入固定在O点的点电荷产生的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面,不计重力,下列判断正确的是( )| A. | 此粒子一定受到静电排斥力的作用 | |
| B. | 粒子在b点的电势能一定小于在a点的电势能 | |
| C. | 粒子在b点的速度一定大于在a点的速度 | |
| D. | 粒子在a点和c点的速度大小一定相等 |

| A. | 弹簧的劲度系数5N/cm | B. | 弹簧的劲度系数0.5N∕cm | ||
| C. | 弹簧的劲度系数50N∕cm | D. | 弹簧的劲度系数500N∕cm |
 如图所示,三只完全相同的灯泡L1、L2、L3分别与电阻R、电容C、电感L串联,再将三者并联,接在220V,50Hz的交变电压两端,三只灯泡亮度相同,若将交变电压的频率改为40Hz,则( )
如图所示,三只完全相同的灯泡L1、L2、L3分别与电阻R、电容C、电感L串联,再将三者并联,接在220V,50Hz的交变电压两端,三只灯泡亮度相同,若将交变电压的频率改为40Hz,则( )| A. | 三只灯泡亮度不变 | B. | 三只灯泡都将变亮 | ||
| C. | L1亮度不变,L2变亮,L3变暗 | D. | L1亮度不变,L2变暗,L3变亮 |
 如图所示,质量为M的半球形容器放在水平面上,O为球心.一质量为m的小滑块,在向右的水平力作用下与容器保持相对静止,并和容器一起水平向右做匀速直线运动.小滑块与容器的接触面是光滑的,容器与地面的接触面是粗糙的,OP与水平方向的夹角为θ.求:
如图所示,质量为M的半球形容器放在水平面上,O为球心.一质量为m的小滑块,在向右的水平力作用下与容器保持相对静止,并和容器一起水平向右做匀速直线运动.小滑块与容器的接触面是光滑的,容器与地面的接触面是粗糙的,OP与水平方向的夹角为θ.求: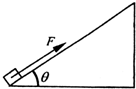 如图所示,已知一足够长粗糙斜面倾角为θ=37°,一质量m=15kg物体,在斜面底部受到一个沿斜面向上的F=300N的力作用由静止开始运动,物体在2秒内位移为20m,2秒末撤销力F,求:(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,已知一足够长粗糙斜面倾角为θ=37°,一质量m=15kg物体,在斜面底部受到一个沿斜面向上的F=300N的力作用由静止开始运动,物体在2秒内位移为20m,2秒末撤销力F,求:(sin37°=0.6,cos37°=0.8,g=10m/s2) 如图所示是一辆火车运动的位移-时间图象.线段OA和BC表示火车做什么运动?线段AB与横轴平行,表示火车做什么运动?火车在4min 内的位移是多少?通过12km用多长时间?火车在中途停了多长时间?
如图所示是一辆火车运动的位移-时间图象.线段OA和BC表示火车做什么运动?线段AB与横轴平行,表示火车做什么运动?火车在4min 内的位移是多少?通过12km用多长时间?火车在中途停了多长时间?