题目内容
(1)如图a所示,一根水平张紧弹性长绳上有等间距的Q′、P′、O、P、Q质点,相邻两质点间距离为lm,t=0时刻O质点从平衡位置开始沿y轴正方向振动,并产生分别向左、向右传播的波,O质点振动图象如b所示,当O点第一次达到正方向最大位移时刻,P点刚开始振动,则______.(填入选项前的字母,有填错的不得分)A.P′、P两点距离为半个波长,因此它们的振动步调始终相反
B.当Q′点振动第一次达到负向最大位移时,O质点已经走过25cm路程
C.当波在绳中传播时,绳中所有质点沿x轴移动的速度大小相等且保持不变
D.若O质点振动加快,周期减为2s,则O点第一次达到正方向最大位移时刻,P点也刚好开始振动
(2)如图所示,一小孩站在宽6m的河边,在他正对面的岸边有一距离河面高度为3m的树,树的正下方河底有一块石头,小孩向河面看去,可同时看到树顶和石头两者的像,并发现两个像重合,若小孩的眼睛离河面高为1.5m,河水的折射率为
 ,试估算河水深度.
,试估算河水深度.

【答案】分析:(1)由题意,波源O产生两列波,同时向左和向右传播,利用对称性,分析P、P′的振动步调.根据Q′的振动情况,确定时间,求出O点运动路程.根据振动图象求周期,由O点的起振情况求出波长,再求出波速.
(2)由题意作出折射光路图,由几何关系及折射定律可求出河水的深度.
解答: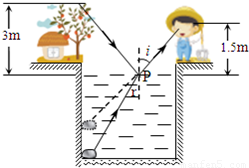 解:(1)A、根据对称性,P与P′步调始终一致.故A错误.
解:(1)A、根据对称性,P与P′步调始终一致.故A错误.
B、Q′起振方向与O点起振方向相同:向上,当Q′点振动第一次达到负向最大位移时,经过 T,而波由O点传到Q时间为
T,而波由O点传到Q时间为 T,故质点O的路程为:
T,故质点O的路程为: ×4A=25cm,故B正确;
×4A=25cm,故B正确;
C、各质点只是上下振动不会左右移动,故C错误;
D、波速由介质决定,故波速不变,周期变化后,O到平衡位置的时间减少,则O点第一次达到正方向最大位移时刻,波还未传到P点,故D错误;
故选B.
(2)解:光路如图,由图得 n=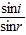 …①
…①
由几何关系得1.5tani+3tani=6
解得 tani=
sini= …②
…②
P点至岸边的距离为:3tani=4m
sinr=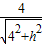 …③
…③
由①②③解得:h=5.3m
答:河水的深度为5.3m.
点评:本题第一小题考查波的传播,注意波速由介质决定,频率与波源决定;
第二小题为光的折射定律的考查,作出光路图,由折射定律及几何关系求解即可.
(2)由题意作出折射光路图,由几何关系及折射定律可求出河水的深度.
解答:
 解:(1)A、根据对称性,P与P′步调始终一致.故A错误.
解:(1)A、根据对称性,P与P′步调始终一致.故A错误.B、Q′起振方向与O点起振方向相同:向上,当Q′点振动第一次达到负向最大位移时,经过
 T,而波由O点传到Q时间为
T,而波由O点传到Q时间为 T,故质点O的路程为:
T,故质点O的路程为: ×4A=25cm,故B正确;
×4A=25cm,故B正确;C、各质点只是上下振动不会左右移动,故C错误;
D、波速由介质决定,故波速不变,周期变化后,O到平衡位置的时间减少,则O点第一次达到正方向最大位移时刻,波还未传到P点,故D错误;
故选B.
(2)解:光路如图,由图得 n=
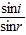 …①
…①由几何关系得1.5tani+3tani=6
解得 tani=

sini=
 …②
…②P点至岸边的距离为:3tani=4m
sinr=
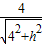 …③
…③由①②③解得:h=5.3m
答:河水的深度为5.3m.
点评:本题第一小题考查波的传播,注意波速由介质决定,频率与波源决定;
第二小题为光的折射定律的考查,作出光路图,由折射定律及几何关系求解即可.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 (1)如图a所示,一根水平张紧弹性长绳上有等间距的Q′、P′、O、P、Q质点,相邻两质点间距离为lm,t=0时刻O质点从平衡位置开始沿y轴正方向振动,并产生分别向左、向右传播的波,O质点振动图象如b所示,当O点第一次达到正方向最大位移时刻,P点刚开始振动,则
(1)如图a所示,一根水平张紧弹性长绳上有等间距的Q′、P′、O、P、Q质点,相邻两质点间距离为lm,t=0时刻O质点从平衡位置开始沿y轴正方向振动,并产生分别向左、向右传播的波,O质点振动图象如b所示,当O点第一次达到正方向最大位移时刻,P点刚开始振动,则




 ,试估算河水深度。
,试估算河水深度。