题目内容
【题目】如图所示，两个半圆柱A、B紧靠着静置于水平地面上，其上有一光滑圆柱C，三者半径均为R．C的质量为m，A、B的质量都为 
，与地面的动摩擦因数均为μ．现用水平向右的力拉A，使A缓慢移动，直至C恰好降到地面．整个过程中B保持静止．设最大静摩擦力等于滑动摩擦力，重力加速度为g．求：
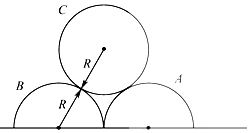
（1）未拉A时，C受到B作用力的大小F；
（2）动摩擦因数的最小值μmin；
（3）A移动的整个过程中，拉力做的功W．
【答案】
（1）
C受力平衡，如图所示：
根据平衡条件可得：2Fcos30°=mg，
解得C受到B作用力的大小为：F= 
；
答：未拉A时，C受到B作用力的大小为 ；
（2）
C恰好降落到地面时，B对C支持力最大为Fm，如图所示，
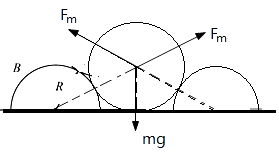
则根据力的平衡可得：2Fmcos60°=mg，
解得：Fm=mg；
所以最大静摩擦力至少为：fm=Fmcos30°= 
，
B对的面的压力为：FN=mBg+ 
=mg，
B受地面的摩擦力为：f=μmg，
根据题意有：fm=f，
解得：μ= 
，
所以动摩擦因数的最小值为：μmin= ；
答：动摩擦因数的最小值为 ；
（3）
C下降的高度为：h= 
，
A的位移为：x= 
，
摩擦力做功的大小为：Wf=fx= 
，
根据动能定理有：W﹣Wf+mgh=0，
解得：W= 
．
答：A移动的整个过程中，拉力做的功W为 ．
【解析】（1）根据共点力的平衡条件求解C受到B作用力的大小F；
（2）先根据共点力平衡条件求解B受到C水平方向最大压力，再求出B对地面的压力，根据摩擦力的计算公式求解；
（3）根据动能定理求解A移动的整个过程中，拉力做的功W．
【考点精析】本题主要考查了滑动摩擦力和动能定理的综合应用的相关知识点，需要掌握滑动摩擦力:利用公式f=μF N 进行计算，其中FN 是物体的正压力，不一定等于物体的重力，甚至可能和重力无关.或者根据物体的运动状态，利用平衡条件或牛顿定律来求解；应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷才能正确解答此题．
