题目内容
5.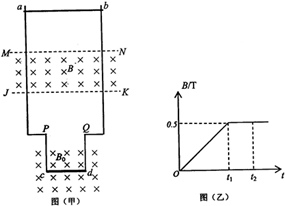 如图所示,两根光滑固定导轨相距0.4m竖直放置,导轨电阻不计,在导轨末端P、Q两点用两根等长的细导线悬挂金属棒cd.棒cd的质量为0.01kg,长为0.2m,处在磁感应强度为B0=0.5T的匀强磁场中,磁场方向垂直于导轨平面向里.相距0.2m的水平线MN和JK之间的区域内存在着垂直导轨平面向里的匀强磁场,且磁感应强度B随时间变化规律如图乙所示.在t=0时刻,质量为0.02kg、阻值为0.3Ω的金属棒ab从虚线MN上方0.2m高处,由静止开始释放,下落过程中保持水平,且与导轨接触良好.结果棒ab在t1时刻从上边界MN进入磁场中做匀速运动,在t2时刻从下边界JK离开磁场,g取10m/s2.求:
如图所示,两根光滑固定导轨相距0.4m竖直放置,导轨电阻不计,在导轨末端P、Q两点用两根等长的细导线悬挂金属棒cd.棒cd的质量为0.01kg,长为0.2m,处在磁感应强度为B0=0.5T的匀强磁场中,磁场方向垂直于导轨平面向里.相距0.2m的水平线MN和JK之间的区域内存在着垂直导轨平面向里的匀强磁场,且磁感应强度B随时间变化规律如图乙所示.在t=0时刻,质量为0.02kg、阻值为0.3Ω的金属棒ab从虚线MN上方0.2m高处,由静止开始释放,下落过程中保持水平,且与导轨接触良好.结果棒ab在t1时刻从上边界MN进入磁场中做匀速运动,在t2时刻从下边界JK离开磁场,g取10m/s2.求:(1)在0~t1时间内,电路中感应电动势的大小;
(2)在t1~t2时间内,棒cd受到细导线的总拉力为多大;
(3)棒cd在0~t2时间内产生的焦耳热.
分析 (1)由自由落体运动运动规律求出ab棒的速度,由法拉第电磁感应定律求出感应电动势.
(2)对ab棒由平衡条件可以求出电流,对cd棒由平衡条件求出拉力.
(3)由E=BLv求出感应电动势,由欧姆定律求出电流,由焦耳定律求出焦耳热.
解答 解:(1)ab棒做自由落体运动,
棒的位移:h=$\frac{1}{2}$gt12,解得:t1=$\sqrt{\frac{2h}{g}}$=0.2s,
磁感应强度的变化率:$\frac{△B}{△t}$=$\frac{0.5B}{0.2s}$=2.5T/s,
0-t1时间内的感应电动势:E1=$\frac{△Φ}{△t}$=$\frac{△B}{△t}$S=$\frac{△B}{△t}$Labh=0.2V;
(2)ab棒匀速进入磁场区域,由平衡条件得:
BI2Lab=mabg,代入数据解得:I2=1A,
在时间t1-t2内,对cd棒,由平衡条件得:
FT=mcdg+B0I2Lcd,代入数据解得:FT=0.2N;
(3)ab棒刚进入磁场时的速度:v=gt1=2m/s,
ab棒刚进入磁场时的感应电动势:E2=BLabv=0.4V,
由图示电路图可知,Rcd=$\frac{{E}_{2}}{{I}_{2}}$-Rab=0.1Ω,
在0-t1内感应电流:I1=$\frac{{E}_{1}}{{R}_{ab}+{R}_{cd}}$=0.5A,
棒cd在0-t2内产生的焦耳热:Qcd=Q1+Q2=I12Rcdt1+I22Rcd•$\frac{h}{v}$=0.015J;
答:(1)在0~t1时间内,电路中感应电动势的大小为0.2V;
(2)在t1~t2时间内,棒cd受到细导线的总拉力为多大为0.2N;
(3)棒cd在0~t2时间内产生的焦耳热为0.015J.
点评 本题是一道力学、电磁感应与电路相结合的综合题,难度较大,分析清楚棒的运动过程、由图示图象求出磁感应强度的变化率是正确解题的关键,应用匀变速运动规律、法拉第电磁感应定律、欧姆定律、安培力公式与平衡条件、焦耳定律可以解题.


| A. | 在0-1s内,合外力做2J的正功 | B. | 在0-2s内,合外力做3.5J的正功 | ||
| C. | 在1-2s内,合外力做1.5J的正功 | D. | 在0-3s内,合外力做正功 |
 一电子在电场中沿图所示从a到b,b到c,c到d,d到e的运动过程中,电场力对电子所做的功分别为+2eV,-8eV,+4eV,-3eV,则上述各点中( )
一电子在电场中沿图所示从a到b,b到c,c到d,d到e的运动过程中,电场力对电子所做的功分别为+2eV,-8eV,+4eV,-3eV,则上述各点中( )| A. | 电势最高的点是e | B. | 电势最高的点是b | ||
| C. | 电子在d点的电势能最小 | D. | 电子在c点的电势能最大 |
| A. | 太阳光本身就是偏振光 | |
| B. | 将一个偏振片对着太阳光慢慢转动一周,透过的光将时明时暗 | |
| C. | 光的偏振现象有力地说明了光是一种波,所以一切波都有偏振现象 | |
| D. | 阳光透过一个固定的偏振片照到第二个偏振片,转动后者看到最后透过的光时明时暗 |

| A. | 图(甲)中因穿过铝环的磁通量始终为零,所以铝环中不产生感应电流 | |
| B. | 图(乙)中地面上方的电场方向和磁场方向可能重合 | |
| C. | 由公式E=N$\frac{△φ}{△t}$可求出图(丙)导线abc中的感应电动势为零 | |
| D. | 图(丁)中,当导线A通过向外的电流时,磁铁对斜面的压力减小,同时弹簧缩短 |
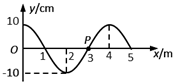 一列简谐横波在t=0时的波形图如图所示,介质中x=3m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(10πt)cm.则关于此波下列说法错误的是( )
一列简谐横波在t=0时的波形图如图所示,介质中x=3m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(10πt)cm.则关于此波下列说法错误的是( )| A. | 波速为20m/s | |
| B. | 沿x轴正方向传播 | |
| C. | t=0.32s时,P点沿y轴负方向振动 | |
| D. | t=2s时的波形图与t=0时的波形图相重叠 |
 在“探究变压器线圈两端电压与匝数的关系”实验中,小张同学进行了下列的操作:
在“探究变压器线圈两端电压与匝数的关系”实验中,小张同学进行了下列的操作: 质量为10kg的物体在一水平推力F作用下,从粗糙斜面的底端由静止开始沿固定斜面向上做匀加速直线运动,加速度大小为5m/s2,2秒钟后撤去该力F.物体与斜面间的动摩擦因数μ=0.25,斜面与水平地面的夹角θ=37°.(已知 sin37°=0.6,cos37°=0.8,g=10m/s2)
质量为10kg的物体在一水平推力F作用下,从粗糙斜面的底端由静止开始沿固定斜面向上做匀加速直线运动,加速度大小为5m/s2,2秒钟后撤去该力F.物体与斜面间的动摩擦因数μ=0.25,斜面与水平地面的夹角θ=37°.(已知 sin37°=0.6,cos37°=0.8,g=10m/s2) 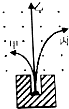 如图所示,放射源放在铅块上的细孔中,铅块上方有匀强磁场,磁场方向度垂直于纸面向外,已知放射源放出的射线有α、β、γ三种,根据图示可以判断出甲是β射线,乙是γ射线.
如图所示,放射源放在铅块上的细孔中,铅块上方有匀强磁场,磁场方向度垂直于纸面向外,已知放射源放出的射线有α、β、γ三种,根据图示可以判断出甲是β射线,乙是γ射线.