��Ŀ����
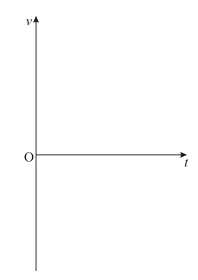
����Ŀ����ͼ�ף�һ�߳�L=2.5m������m=0.5kg�������ν����߿��ڹ⻬��Ե��ˮƽ���ϣ�����װ�÷�����ֱ���ϡ��Ÿ�Ӧǿ��ΪB=0.8T����ǿ�ų��У�����һ����ų��ı߽�MN�غϣ���ˮƽ��F�������ɾ�ֹ��ʼ�����˶�������5s�߿������ų�����ý����߿��еĵ�����ʱ��仯��ͼ����ͼ����ʾ���ڽ����߿������Ĺ����С�
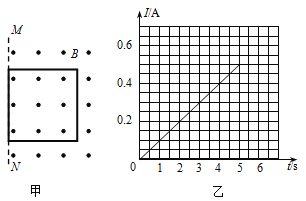
��1����ͨ���߿����ĵ�������߿�ĵ��裻
��2����֪����5s����F����1.92J����ô�ڴ˹����У��߿�����Ľ������Ƕ��٣�
��3�������߿��뿪�ų�ʱ����F�Ĵ�С��
���𰸡���1��![]()
![]() ��2��
��2��![]() ��3��
��3��![]()
���������������������ͼ������������Ӧ�÷����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɡ���������ʽ����������Ȼ�����������ֵ����ͼ�����������ʱ��仯�Ĺ�ϵ������ŷķ�������������Ȼ��������ٶȣ�Ȼ����ţ�ٵڶ�������������ı���ʽ���������غ㶨�ɿ�������߿�����Ľ�������
��1��I-tͼ���������Χ�������ͨ���߿����ĵ��������ͼb��ʾͼ���֪��ͨ���߿����ĵ����� ![]() ,�������
,������� ![]() ���������ݽ�ã�
���������ݽ�ã� ![]()
��2����t=5sʱ���߿�Ӵų����������ٶ���v5=at=1m/s���߿��в���������Ϊ�� ![]() .
.
��3����ͼ��ʾͼ���֪��I=0.1t���ɸ�Ӧ������ ![]() ���ɵý�������ٶ�Ҳ�����Եģ��ɵ�
���ɵý�������ٶ�Ҳ�����Եģ��ɵ�![]() �����߿�ļ��ٶ�Ϊ��a=0.2m/s2���߿��������Ͱ��������������ȼ����˶�����
�����߿�ļ��ٶ�Ϊ��a=0.2m/s2���߿��������Ͱ��������������ȼ����˶�����![]()
�ɵ��� ![]()
������ ![]() ���������ݽ�ã�t=5s
���������ݽ�ã�t=5s
�����߿��뿪�ų�ʱ����F�Ĵ�СΪ�� ![]()

 ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�