题目内容
5. 如图所示,半径为R的半圆柱形玻璃柱,放置在直角坐标系xoy中,圆心与坐标系原点O重合,在第二象限中坐标为(-1.5R,$\frac{{\sqrt{3}}}{2}$R)的点A处,放置一个激光器(图中未画出),发出的两束细激光束a和b,其中,激光束a平行于x轴射向玻璃砖,激光束b沿AO方向射向玻璃砖.已知激光在玻璃中的折射率为$\sqrt{3}$,试作出激光束a和b通过玻璃砖的光路图,并证明a和b射出玻璃砖后是否相交.
如图所示,半径为R的半圆柱形玻璃柱,放置在直角坐标系xoy中,圆心与坐标系原点O重合,在第二象限中坐标为(-1.5R,$\frac{{\sqrt{3}}}{2}$R)的点A处,放置一个激光器(图中未画出),发出的两束细激光束a和b,其中,激光束a平行于x轴射向玻璃砖,激光束b沿AO方向射向玻璃砖.已知激光在玻璃中的折射率为$\sqrt{3}$,试作出激光束a和b通过玻璃砖的光路图,并证明a和b射出玻璃砖后是否相交.
分析 两光束经过两次折射射入空气,画出光路图.根据几何知识得到两光束的入射角,由折射定律求出折射角,结合数学知识判断a和b射出玻璃砖后是否相交.
解答 解:激光束a、b经过玻璃砖的折射光路图如图所示: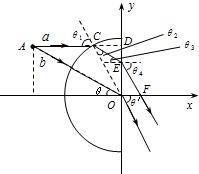
如图,tanθ=$\frac{\frac{\sqrt{3}}{2}R}{1.5R}$=$\frac{\sqrt{3}}{3}$,得θ=30°
激光束b:
在O点有:n=$\frac{sinθ′}{sinθ}$,得 θ′=60°
又 sinθ1=$\frac{\frac{\sqrt{3}}{2}R}{R}$=$\frac{\sqrt{3}}{2}$,得 θ1=60°
激光束a:在C点有:n=$\frac{sin{θ}_{1}}{sin{θ}_{2}}$,得 θ2=30°
在E点有:n=$\frac{sin{θ}_{4}}{sin{θ}_{3}}$=$\frac{sin{θ}_{4}}{sin({θ}_{1}-{θ}_{2})}$,得 θ4=60°
由θ4=θ′,两束光射出后应平行,故不相交.
答:光路图如图所示,a和b射出玻璃砖后不相交.
点评 本题是几何光学问题,画出光路图,运用折射定律和几何知识结合进行求解,是常规方法.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
15. 如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )
如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )
 如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )
如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )| A. | a、b、c、d四点电势不等,但电场强度相等 | |
| B. | 若一电子从b点运动到c点,克服电场力做的功为0.4eV | |
| C. | 若一电子从左侧沿中心轴线穿越电场区域,将做加速度先增加后减小的加速直线运动 | |
| D. | 若一束电子从左侧平行于中心轴线进入电场区域,将会从右侧平行于中心轴线穿出 |
16.在LC电磁振荡回路中,电容两端的电压u随时间t变化的规律如图所示,则( )


| A. | 在时刻t1,电路中的磁场能最小 | |
| B. | 在时刻t2,电路中的磁场能最小 | |
| C. | 从时刻t2至t3,在电路中磁场能转化为电场能 | |
| D. | 从时刻t2至t3,在电路中电场能转化为磁场能 |
13. 如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
 如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )| A. | 在该过程中,物块也做匀速运动 | B. | 人对物块做功$\frac{1}{2}$mv02 | ||
| C. | 人对物块做功$\frac{{m{V_0}^2{S^2}}}{{2({h^2}+{S^2})}}$ | D. | 物块运动的速率为$\frac{{{V_0}h}}{{\sqrt{{h^2}+{S^2}}}}$ |
20.已知地球半径约为6.4×106米,又知月球绕地球的运动可近似看作匀速圆周运动,则可估算出月球到地心的距离约为:(结果只保留一位有效数字)( )
| A. | 1×108m | B. | 4×108m | C. | 7×108m | D. | 9×108m |
14.物理学发展的过程中,许多物理学家的科学发现推动了人类历史的进步.以下叙述中,正确的说法是( )
| A. | 开普勒发现万有引力定律 | |
| B. | 爱因斯坦提出:在一切惯性参照物中,测量到的真空中的光速c都一样 | |
| C. | 牛顿利用扭秤实验,首先测出引力常量,为人类实现飞天梦想奠定了基础 | |
| D. | 相对论的创立表明经典物理学已不再适用 |
15.在同一高度将质量相等的三个小球以大小相同的速度分别竖直上抛、竖直下抛、水平抛出,不计空气阻力.从抛出到落地过程中,三球( )
| A. | 运动时间相同 | B. | 落地时的动能相同 | ||
| C. | 落地时重力的功率相同 | D. | 同落地时的速度相同 |

 如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,那么:
如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,那么: