题目内容
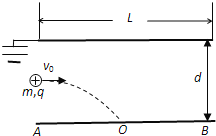
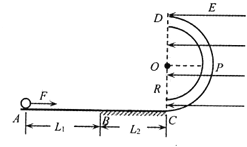
【题目】如图所示,固定在竖直平面内的绝缘细半圆管轨道在C点与绝缘的水平地面平滑连接,半圆管的半径R=1.6m,管内壁光滑,两端口C,D连线沿竖直方向,CD右侧存在场强大小E=1.5×103N/C、方向水平向左的匀强电场;水平面AB段表面光滑,长L1=6.75m,BC段表面粗糙,长L2=5.5m.质量m=2.0kg、电荷量q=0.01C的带正电小球在水平恒力F=10.0N的作用下从A点由静止升始运动,经过一段时间后撤去拉力F,小球进人半圆管后通过端口D时对圆管内轨道有竖直向下的压力ND=15N.小球与水平面BC段之间的动摩擦因数u=0.2,取g=10m/s2.求:
(1)小球通过端口D时的速度大小vD;
(2)小球通过半圆管中点P时与圆管的作用力大小NP;
(3)撤去拉力F时小球的速度大小v0.
【答案】(1)2m/s(2)0(3)9 m/s
【解析】试题分析:(1)在端口D由牛顿第二定律有![]()
解得:![]()
(2)设小球经过半圆管中点P时的速度大小为vP,从P到D的过程中由动能定理可得
qER-mgR=![]() mvD2-
mvD2-![]() mvP2
mvP2
解得vP=2![]() m/s
m/s
在P点由牛顿第二定律有![]()
解得NP=0
(3)设F作用的距离为s,从A到D由动能定理有
Fs-μmgL2-2mgR=![]() mvD2
mvD2
解得s="9" m
在F作用的过程中由动能定理得Fs-μmg(s-L1)=![]() mv02
mv02
解得v0="9" m/s

练习册系列答案
相关题目