题目内容
15. 如图所示,水平转台上有一个质量为2kg的物块,用长为0.8m的细绳将物块连接在转轴上,细线与竖直转轴的夹角θ为60°角,此时绳中张力为零,物块与转台间动摩擦因数为0.5,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,重力加速度g取10m/s2则( )
如图所示,水平转台上有一个质量为2kg的物块,用长为0.8m的细绳将物块连接在转轴上,细线与竖直转轴的夹角θ为60°角,此时绳中张力为零,物块与转台间动摩擦因数为0.5,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,重力加速度g取10m/s2则( )| A. | 至绳中出现拉力时,转台对物块做的功为$2\sqrt{3}$J | |
| B. | 至绳中出现拉力时,转台对物块做的功为$\sqrt{3}$J | |
| C. | 至转台的角速度增大到5rad/s时,物块机械能增量为24J | |
| D. | 至转台对物块支持力为零时,转台对物块做的功为12J |
分析 对物体受力分析知物块离开圆盘前:合力F=f+Tsinθ=$m\frac{{v}^{2}}{r}$,N+Tcosθ=mg,根据动能定理知W=Ek=$\frac{1}{2}m{v}^{2}$,然后根据临界条件分析做功和机械能变化.
解答 解:A、对物体受力分析知物块离开圆盘前
合力F=f+Tsinθ=$m\frac{{v}^{2}}{r}$①
N+Tcosθ=mg②
根据动能定理知W=Ek=$\frac{1}{2}m{v}^{2}$③
AB、当弹力T=0,r=Lsinθ④
由①②③④解得W=$\frac{1}{2}$fLsinθ≤$\frac{1}{2}μmgLsinθ$
至绳中出现拉力时,转台对物块做的功为W=$\frac{1}{2}$μmgLsinθ=$2\sqrt{3}$J,故A正确,B错误;
C、当物块刚好离开转台时,由重力和绳子拉力的合力提供向心力,则有:
mgtan60°=m${{ω}_{0}}^{2}Lsin60°$
解得:ω0=$\sqrt{\frac{g}{Lcosθ}}$=5rad/s,
则转台的角速度增大到5rad/s时,物块刚好离开转台,重力势能不变,
物块机械能增量$△E={△E}_{K}=\frac{1}{2}m({ω}_{0}Lsin60°)^{2}$=$\frac{1}{2}×2×{(5×0.8×\frac{\sqrt{3}}{2})}^{2}=12J$,故C错误;
D、当N=0,f=0,由①②③知W=$\frac{1}{2}$mgLsinθtanθ=$\frac{1}{2}×2×10×0.8×\frac{\sqrt{3}}{2}×\sqrt{3}=12J$,故D正确;
故选:AD
点评 此题考查牛顿运动定律和功能关系在圆周运动中的应用,注意临界条件的分析,至绳中出现拉力时,摩擦力为最大静摩擦力;转台对物块支持力为零时,N=0,f=0.题目较难,计算也比较麻烦.

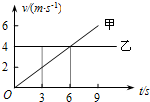
| A. | t=0时乙在甲的前方9 m处 | B. | t=0时甲在乙的前方9 m处 | ||
| C. | 3s之后两物体还会再相遇 | D. | 3 s之后两物体不会再相遇 |
 如图所示,水平恒力F拉着质量为m的木块在水平放置在地面上的长木板上向右匀速运动,木板恰好能保持静止.则在此基础上,再逐渐增大F的过程中(设木板足够长,木块没脱离木板),则关于木板与地面之间的摩擦力大小的说法正确的是( )
如图所示,水平恒力F拉着质量为m的木块在水平放置在地面上的长木板上向右匀速运动,木板恰好能保持静止.则在此基础上,再逐渐增大F的过程中(设木板足够长,木块没脱离木板),则关于木板与地面之间的摩擦力大小的说法正确的是( )| A. | 恒为开始的F | |
| B. | 随F的增大而增大 | |
| C. | 由于木板没有运动,所以没有摩擦力 | |
| D. | 由于木板和地面的粗糙程度不知道,所以无法判断 |
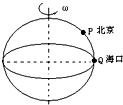 如图所示是地球示意图,由于地球的自转,地球表面上P点北京、Q点海口两地均绕地球自转轴做匀速圆周运动,对于北京、Q海口两地的运动,下列说法正确的是( )
如图所示是地球示意图,由于地球的自转,地球表面上P点北京、Q点海口两地均绕地球自转轴做匀速圆周运动,对于北京、Q海口两地的运动,下列说法正确的是( )| A. | 北京、海口两地的线速度大小相等 | |
| B. | 北京转动的线速度比海口的线速度大 | |
| C. | 北京、海口两地的角速度大小相等 | |
| D. | 北京的转动的角速度比海口的角速度大 |
| A. | 动能为$\frac{1}{2}m{v^2}+mg(H-h)$ | B. | 重力势能为mg(H-h) | ||
| C. | 机械能为$\frac{1}{2}m{v^2}+mgh$ | D. | 机械能为$\frac{1}{2}m{v^2}+mgH$ |
| A. | 物体的温度越高,分子热运动越剧烈,分子平均动能越大,且每一个分子的动能越大 | |
| B. | 布朗运动就是液体分子的热运动 | |
| C. | 一切达到热平衡的系统一定具有相同的内能 | |
| D. | 分子间的距离r存在某一值r0,当r<r0时,斥力大于引力,当r>r0时,引力大于斥力 |
 如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B,D间的距离为h,则下列说法正确的是( )
如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B,D间的距离为h,则下列说法正确的是( )| A. | A,B两点间的距离为$\frac{h}{2}$ | B. | A,B两点间的距离为$\frac{h}{3}$ | ||
| C. | C,D两点间的距离为$\frac{2\sqrt{3}}{3}$h | D. | C,D两点间的距离为2h |
| A. | 3.0×104 V | B. | 2.0×104 V | C. | 1.0×104 V | D. | 4.0×104 V |
 高速铁路简称“高铁”,是指通过改造原有线路(弯道直线化、轨距标准化),使最高营运速率达到不小于每小时200公里.如图若某列高铁在一个半径为4km的弯道转弯时由于轨道面倾斜使得车体倾斜θ=150左右,恰好轨道内外侧都无挤压(取tan15°=0.25,g=10m/s2),则此时火车的转弯时的速度是多大?
高速铁路简称“高铁”,是指通过改造原有线路(弯道直线化、轨距标准化),使最高营运速率达到不小于每小时200公里.如图若某列高铁在一个半径为4km的弯道转弯时由于轨道面倾斜使得车体倾斜θ=150左右,恰好轨道内外侧都无挤压(取tan15°=0.25,g=10m/s2),则此时火车的转弯时的速度是多大?