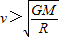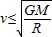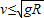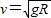Question

一行星质量为M，半径是R，表面的重力加速度是g．卫星绕它做匀速圆周运动的速率是v，若万有引力恒量为G，则（　　）

• A．v＞

  GM R

• B．v≤

  GM R

• C．v≤

  gR

• D．v=

  gR

Answer 1

分析：根据万有引力提供向心力，结合万有引力等于重力，求出线速度与轨道半径的关系，从而确定正确的答案．

解答：解：根据万有引力提供向心力得，G

Mm

r2

=m

v2

r

，解得v=

GM r

，知轨道半径越小，则线速度最大，则卫星绕行星做圆周运动的最大速率v=

GM R

．因为GM=gR²，所以v=

gR

．则v≤

GM R

=

gR

．故B、C正确，A、D错误．
故选BC．

点评：解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论，并能灵活运用．