题目内容
7.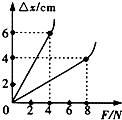 在“探究弹力和弹簧伸长的关系”的实验中,某同学取了两根弹簧进行实验,根据测得的数据绘出了如图所示的图象,从图象可以看出图象的上端发生了弯曲,这是由于弹力超越了弹簧的弹性限度;其中,较粗的弹簧的劲度系数为200N/m;如果用这两根弹簧来做“验证力的平行四边形定则”的实验,实验中在保证两根弹簧均不损坏的情况下,并且要求两根弹簧间的夹角为$\frac{π}{2}$,那么,这两根弹簧的最大合力为4$\sqrt{5}$N(保留根号)
在“探究弹力和弹簧伸长的关系”的实验中,某同学取了两根弹簧进行实验,根据测得的数据绘出了如图所示的图象,从图象可以看出图象的上端发生了弯曲,这是由于弹力超越了弹簧的弹性限度;其中,较粗的弹簧的劲度系数为200N/m;如果用这两根弹簧来做“验证力的平行四边形定则”的实验,实验中在保证两根弹簧均不损坏的情况下,并且要求两根弹簧间的夹角为$\frac{π}{2}$,那么,这两根弹簧的最大合力为4$\sqrt{5}$N(保留根号)
分析 根据胡克定律结合数学知识即可正确解答,力的合成的法则.
解答 解:从图象可以看出图象的上端发生了弯曲,这是由于弹力超越了弹簧的 弹性限度;斜率的倒数表示弹簧的劲度系数,则较粗的弹簧的劲度系数为k=$\frac{△F}{△x}$=$\frac{8}{0.04}$=200N/m,
两根弹簧间的夹角为$\frac{π}{2}$,这两根弹簧的最大合力为:F=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$N
故答案为:弹性限度;200;4$\sqrt{5}$
点评 本题考查了弹簧弹力F和弹簧伸长量x的关系的基础知识,比较简单,是一道考查基础知识的好题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.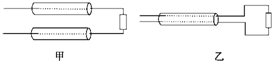 某输电线路横穿公路时,要在地下埋线通过,为了保护线路不至于被压坏,预先铺设结实的过路钢管,再让输电线从钢管中穿过,电线穿管的方案有两种,甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过,乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过,如果输电导线输送的电流很强大,以下说法正确的是( )
某输电线路横穿公路时,要在地下埋线通过,为了保护线路不至于被压坏,预先铺设结实的过路钢管,再让输电线从钢管中穿过,电线穿管的方案有两种,甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过,乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过,如果输电导线输送的电流很强大,以下说法正确的是( )
 某输电线路横穿公路时,要在地下埋线通过,为了保护线路不至于被压坏,预先铺设结实的过路钢管,再让输电线从钢管中穿过,电线穿管的方案有两种,甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过,乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过,如果输电导线输送的电流很强大,以下说法正确的是( )
某输电线路横穿公路时,要在地下埋线通过,为了保护线路不至于被压坏,预先铺设结实的过路钢管,再让输电线从钢管中穿过,电线穿管的方案有两种,甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过,乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过,如果输电导线输送的电流很强大,以下说法正确的是( )| A. | 无论输送的电流是恒定电流还是交变电流,甲乙两方案都是可行的 | |
| B. | 若输送的电流是恒定电流,甲方案是可行的,乙方案是不可行的 | |
| C. | 若输送的电流是交变电流,乙方案是可行的,甲方案是不可行的 | |
| D. | 若输送的电流是交变电流,甲方案是可行的,乙方案是不可行的 |
18.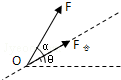 某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
 某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )| A. | 加速时动力的大小等于mg | |
| B. | 加速与减速时的加速度大小之比为2:$\sqrt{3}$ | |
| C. | 减速飞行时间t后速度为零 | |
| D. | 加速与减速过程发生的位移大小之比为1:2 |
15.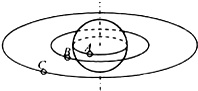 如图所示,A是静止在赤道上的物体,随地球自转而做匀速圆周运动;B、C是同一平面内两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是地球同步卫星.已知第一宇宙速度为v,物体A和卫星B、C的线速度大小分别为vA、vB、vC,周期大小分别为TA、TB、TC,则下列关系正确的是( )
如图所示,A是静止在赤道上的物体,随地球自转而做匀速圆周运动;B、C是同一平面内两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是地球同步卫星.已知第一宇宙速度为v,物体A和卫星B、C的线速度大小分别为vA、vB、vC,周期大小分别为TA、TB、TC,则下列关系正确的是( )
 如图所示,A是静止在赤道上的物体,随地球自转而做匀速圆周运动;B、C是同一平面内两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是地球同步卫星.已知第一宇宙速度为v,物体A和卫星B、C的线速度大小分别为vA、vB、vC,周期大小分别为TA、TB、TC,则下列关系正确的是( )
如图所示,A是静止在赤道上的物体,随地球自转而做匀速圆周运动;B、C是同一平面内两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是地球同步卫星.已知第一宇宙速度为v,物体A和卫星B、C的线速度大小分别为vA、vB、vC,周期大小分别为TA、TB、TC,则下列关系正确的是( )| A. | vA=vC=v | B. | vA<vC<vB<v | C. | TA<TC<TB | D. | TA<TB<TC |
19.一列沿x轴正方向传播的简谐横波在t=0时刻的波形图如图甲所示,P点离原点O距离为x1=2m的一个介质质点,Q质点离原点O的距离x2=4m,此时离原点O距离x3=6m的介质质点刚刚要开始振动.图乙是该简谐波传播方向上的某一质点的振动图象(与甲计时起点相同).由此可知,下列说法正确的是( )
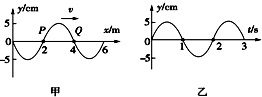

| A. | 这列波的波长为λ=2m | |
| B. | 乙图可能是图甲中质点Q的振动图象 | |
| C. | 这列波的传播速度为v=3m/s | |
| D. | 这列波的波源起振方向为向下 |
16.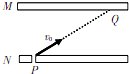 如图所示,水平放置的平行板电容器,两板间距为d.带负电的小球质量为m,带电量为q,从下极板N的小孔P处,以初速度v0射入,沿直线到达上极板M上的小孔Q,若重力加速度为g.则( )
如图所示,水平放置的平行板电容器,两板间距为d.带负电的小球质量为m,带电量为q,从下极板N的小孔P处,以初速度v0射入,沿直线到达上极板M上的小孔Q,若重力加速度为g.则( )
 如图所示,水平放置的平行板电容器,两板间距为d.带负电的小球质量为m,带电量为q,从下极板N的小孔P处,以初速度v0射入,沿直线到达上极板M上的小孔Q,若重力加速度为g.则( )
如图所示,水平放置的平行板电容器,两板间距为d.带负电的小球质量为m,带电量为q,从下极板N的小孔P处,以初速度v0射入,沿直线到达上极板M上的小孔Q,若重力加速度为g.则( )| A. | 小球在M、N间运动的加速度不为零 | B. | M板电势高于N板电势 | ||
| C. | 小球从P到Q,电势能增加了mgd | D. | M、N间电势差大小为$\frac{mgd}{q}$ |
17.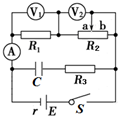 在如图所示的电路中,电源的电动势为E,内阻为r,R1、R3为定值电阻,R2为滑动变阻器,C为电容器.将滑动变阻器的滑动触头P置于位置a,闭合开关S,电路稳定时理想电压表V1、V2的示数分别为U1、U2,理想电流表A的示数为I.当滑动变阻器的滑动触头P由a滑到b且电路再次稳定时,理想电压表V1、V2的示数分别为U1′、U2′,理想电流表A的示数为I'.则以下判断中正确的是( )
在如图所示的电路中,电源的电动势为E,内阻为r,R1、R3为定值电阻,R2为滑动变阻器,C为电容器.将滑动变阻器的滑动触头P置于位置a,闭合开关S,电路稳定时理想电压表V1、V2的示数分别为U1、U2,理想电流表A的示数为I.当滑动变阻器的滑动触头P由a滑到b且电路再次稳定时,理想电压表V1、V2的示数分别为U1′、U2′,理想电流表A的示数为I'.则以下判断中正确的是( )
 在如图所示的电路中,电源的电动势为E,内阻为r,R1、R3为定值电阻,R2为滑动变阻器,C为电容器.将滑动变阻器的滑动触头P置于位置a,闭合开关S,电路稳定时理想电压表V1、V2的示数分别为U1、U2,理想电流表A的示数为I.当滑动变阻器的滑动触头P由a滑到b且电路再次稳定时,理想电压表V1、V2的示数分别为U1′、U2′,理想电流表A的示数为I'.则以下判断中正确的是( )
在如图所示的电路中,电源的电动势为E,内阻为r,R1、R3为定值电阻,R2为滑动变阻器,C为电容器.将滑动变阻器的滑动触头P置于位置a,闭合开关S,电路稳定时理想电压表V1、V2的示数分别为U1、U2,理想电流表A的示数为I.当滑动变阻器的滑动触头P由a滑到b且电路再次稳定时,理想电压表V1、V2的示数分别为U1′、U2′,理想电流表A的示数为I'.则以下判断中正确的是( )| A. | 滑动变阻器的滑动触头P由a滑向b的过程中,电容器的带电量减小 | |
| B. | 滑动变阻器的滑动触头P由a滑向b的过程中,通过R3的电流方向由右向左 | |
| C. | U1>U1′,U2>U2′,I>I′ | |
| D. | $|{\frac{{{U_2}-{{U'}_2}}}{I-I'}}$|=R1+r |