题目内容

5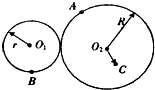．如图所示，半径分别为r和R的两根圆柱靠摩擦传动，已知R=2r，A、B分别在大、小圆柱的边缘上，O2C=r，若两圆柱之间没有出现打滑现象，则A、B、C三点的角速度的比值分别为（　　）
A．2：1：2B．2：2：1C．1：1：2D．1：2：1

分析 解答本题应明确：两轮子靠传送带传动，轮子边缘上的点具有相同的线速度；共轴转动的点，具有相同的角速度．

解答 解：传动过程中，两圆柱之间没有打滑现象，说明A、B两点的线速度相等，即vA=vB
根据题意rA：rB=2：1；
根据v=ωr，有ωA：ωB=1：2；
故ωA：ωB：ωC=1：2：1；
故选：D．

点评 解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点具有相同的角速度；同时结合线速度与角速度关系公式v=ωr列式求解．

练习册系列答案
相关题目
15．如图1所示为山丹一中两位同学探究“物体的加速度与其质量、所受合外力的关系”的实验装置图．

（1）实验中，两位同学安装好实验装置后，首先平衡摩擦力，他们将长木板的一端适当垫高些后，在不挂砝码盘的情况下，使小车靠近打点计时器后，先接通电源，后用手轻拨小车，小车便拖动纸带在木板上自由运动．若打点计时器第一次在纸带上打出的计时点越来越稀疏（从打出的点的先后顺序看），则第二次打点前应将长木板底下的小木块垫的比原先更加低（选填“高”或“低”）些；重复以上操作步骤，直到打点计时器在纸带上打出一系列间隔均匀的计时点，便说明平衡摩擦力合适．
（2）平衡摩擦力后，在盘及盘中砝码的总质量远小于小车质量的条件下，两位同学可以认为砝码盘（连同砝码）的总重力近似等于小车的所受的合外力．
（3）接下来，这两位同学先保持小车的质量不变的条件下，研究小车的加速度与受到的合外力的关系；图2为某次操作中打出的一条纸带，他们在纸带上标出了5个计数点，在相邻的两个计数点之间还有4个点未标出，图中数据的单位是cm．实验中使用的是频率f=50Hz的交变电流．根据以上数据，可以算出小车的加速度a=0.343m/s2．（结果保留三位有效数字）
（4）然后，两位同学在保持小车受到的拉力不变的条件下，研究小车的加速度a与其质量M的关系．他们通过给小车中增加砝码来改变小车的质量M，得到小车的加速度a与质量M的数据，画出a-$\frac{1}{M}$图线后，发现：当$\frac{1}{M}$较大时，图线发生弯曲．于是，两位同学又对实验方案进行了进一步地修正，避免了图线的末端发生弯曲的现象，那么，两位同学的修正方案可能是C
A．改画a与（M+m）的关系图线     B．改画a与$\frac{m}{M}$的关系图线
C．改画a与$\frac{1}{M+m}$的关系图线       D．改画a与$\frac{1}{（M+m）^{2}}$的关系图线
（5）探究“物体的加速度与其质量、所受合外力的关系”实验完成后，两位同学又打算测出小车与长木板间的动摩擦因数．于是两位同学先取掉了长木板右端垫的小木块，使得长木板平放在了实验桌上，并把长木板固定在实验桌上，具体的实验装置如图3所示；在砝码盘中放入适当的砝码后，将小车靠近打点计时器，接通电源后释放小车，打点计时器便在纸带上打出了一系列的点，并在保证小车的质量M、砝码（连同砝码盘）的质量m不变的情况下，多次进行实验打出了多条纸带，分别利用打出的多条纸带计算出了小车运动的加速度a，并求出平均加速度$\overline{a}$，则小车与长木板间的动摩擦因数μ=$\frac{mg-（m+M）\overline{a}}{Mg}$．（用m、M、$\overline{a}$、g表示）
16．物体以速度v匀速通过直线上的A、B两点，所用时间为t现在物体从A点由静止出发，先做匀加速直线运动（加速度为a1）到某一最大速度vm，然后立即做匀减速直线运动（加速度大小为a2）至B点速度恰好减为0，所用时间仍为t．则物体的（　　）
A．vm可为许多值，与al、a2的大小有关B．vm只可为2V，与a1、a2的大小无关
C．a1、a2必须满足$\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{2v}{t}$D．a1、a2必须满足$\frac{2{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{v}{t}$
13．如图所示，通有向左电流的直导线置于匀强磁场中，导线与磁场方向平行，则该导线（　　）
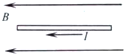
A．不受安培力B．受安培力，方向向右
C．受安培力，方向垂直纸面向里D．受安培力，方向垂直纸面向外
20．一物体在水平面上以恒定加速度运动，位移与时间的关系x=24t─6t2，则其速度为零的时刻是（　　）
A．4s末B．2s末C．6s末D．24s末
10．下列物理量中属于矢量的是（　　）
A．加速度B．速率C．路程D．温度
17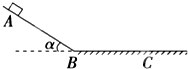．如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据，请充分利用这些数据，求：（重力加速度g=10m/s2 ）
t（s）0.00.20.4…1.21.4…
v（m/s）0.01.02.0…1.10.7…
（1）物体在AB段和在BC段的加速度a1和a2的大小；
（2）物体运动到B点所用时间t1及达到B点的速率VB．
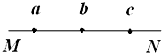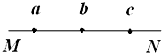14．如图所示，MN是一负的点电荷电场中的一条电场线，场强方向由M指向N，ab=bc，a、b、c三点的场强和电势分别为Ea、Eb、Ec和ϕa、ϕb、ϕc，则下列关系正确的是（　　）
A．Ea＞Eb＞EcB．Ea=Eb=EcC．ϕa＞ϕb＞ϕcD．Uab=Ubc
15．下列说法正确的是（　　）
A．卢瑟福通过α粒子散射实验提出了原子的核式结构模型
B．结合能越大，原子核结构一定越稳定
C．若使用某种频率的光不能使某金属发生光电效应，则需增大入射光光照强度才行
D．发生β衰变时，元素原子核的质量数不变，电荷数增加1
E．将核子束缚在原子核内的核力，是不同于万有引力和电磁力的另一种相互作用

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网