题目内容
4.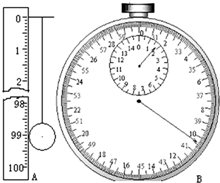 (1)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=$\frac{4{π}^{2}L}{{T}^{2}}$.让刻度尺的零点对准摆线的悬点,摆线竖直下垂,如图所示,那么单摆摆长是99.05cm.如果测定了40次全振动的时间如图中秒表所示,那么秒表读数是100.4s,
(1)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=$\frac{4{π}^{2}L}{{T}^{2}}$.让刻度尺的零点对准摆线的悬点,摆线竖直下垂,如图所示,那么单摆摆长是99.05cm.如果测定了40次全振动的时间如图中秒表所示,那么秒表读数是100.4s,(2)下列给出的材料中应选择BC作为摆球与摆线,组成单摆.
A.木球 B.铁球
C.柔软不易伸长的丝线 D.粗棉线
(3)实验中,测得重力加速度的值较当地重力加速度的值偏大,可能的原因是D
A.摆球的质量偏大B.单摆振动的振幅偏小
B.开始计时时,秒表过早按下
C.计算摆长时没有加上摆球的半径值
D.将实际振动次数n次误记成(n+1)次.
分析 (1)根据T=2$π\sqrt{\frac{L}{g}}$,可知g的表达式.摆长是悬点到球心的距离.秒表的读数等于小盘读数加上大盘读数.
(2)单摆在摆动的过程中摆长不能变,空气阻力能忽略.
(3)根据g=$\frac{4{π}^{2}L}{{T}^{2}}$,分析g值偏大的原因.
解答 解:(1)根据T=2$π\sqrt{\frac{L}{g}}$,知g=$\frac{4{π}^{2}L}{{T}^{2}}$.单摆的摆长是悬点到球心的距离,为99.05cm.秒表小盘读数为90s,大盘读数为10.4s,所以秒表读数为100.4s.
(2)单摆在摆动过程中.阻力要尽量小甚至忽略不计,所以摆球选铁球;摆动时摆长不变,所以选柔软不易伸长的丝线.故B、C正确,A、D错误.
故选BC.
(3)A、由公式可知,周期与摆球的质量无关;故A错误;
B、开始计时时,秒表过早按下.测得时间偏长,周期偏大,根据g=$\frac{4{π}^{2}L}{{T}^{2}}$,测得重力加速度偏小.故B错误.
C、计算摆长时没有加上摆球的半径值,测得的摆长偏小,根据g=$\frac{4{π}^{2}L}{{T}^{2}}$,测得重力加速度偏小.故C错误.
D、将实际振动次数n次误记成(n+1)次.测得的周期偏小,根据g=$\frac{4{π}^{2}L}{{T}^{2}}$,测得的重力加速度偏大.故D正确.
故选D.
故答案为:(1)$\frac{4{π}^{2}L}{{T}^{2}}$,99.05cm,100.4;(2)BC;(3)D.
点评 本题考查用单摆测定重力加速度的实验;解决本题的关键掌握单摆的周期公式T=2$π\sqrt{\frac{L}{g}}$,以及知道测量时形成误差的原因.

练习册系列答案
相关题目
9.以下说法正确的是( )
| A. | 变速运动一定是曲线运动 | |
| B. | 曲线运动一定是变速运动 | |
| C. | 速率不变的曲线运动是匀速运动 | |
| D. | 曲线运动中质点的运动状态可能不发生变化 |
 如图所示,有一质量为M的木板(足够长)静止在光滑的水平面上,一质量为m的小铁块以初速度v0水平滑上木板的左端,小铁块与木板之间的动摩擦因数为μ,若小铁块恰好没有滑离木板,求
如图所示,有一质量为M的木板(足够长)静止在光滑的水平面上,一质量为m的小铁块以初速度v0水平滑上木板的左端,小铁块与木板之间的动摩擦因数为μ,若小铁块恰好没有滑离木板,求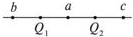 如图所示,Q1=2×10-12C、Q2=-4×10-12C,Q1、Q2相距12cm,求a、b、c三点的电场强度大小和方向,其中a为Q1Q2连线的中点,b为Q1左方6cm处的点,c为Q2右方6cm处的点.
如图所示,Q1=2×10-12C、Q2=-4×10-12C,Q1、Q2相距12cm,求a、b、c三点的电场强度大小和方向,其中a为Q1Q2连线的中点,b为Q1左方6cm处的点,c为Q2右方6cm处的点.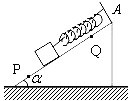 在探究物体间的最大静摩擦力的实验中,有一种测量最大静摩擦力的方法:如图所示,倾角为α的斜面上,用一根劲度系数k=100N/m的弹簧平行于斜面方向拴住一个质量为m的物体,发现物体仅在PQ之间任何位置都能处于静止状态,若测得AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小.
在探究物体间的最大静摩擦力的实验中,有一种测量最大静摩擦力的方法:如图所示,倾角为α的斜面上,用一根劲度系数k=100N/m的弹簧平行于斜面方向拴住一个质量为m的物体,发现物体仅在PQ之间任何位置都能处于静止状态,若测得AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小.