题目内容
(14分)如图所示,质量为m=2kg的小球穿在长L=1m的轻杆顶部,轻杆与水平方向成θ=37°的夹角,将小球由静止释放,1s后小球恰好到达轻杆底端,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
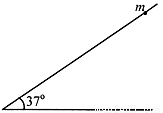
⑴小球到达杆底时重力对它做功的功率;
⑵小球与轻杆之间的动摩擦因数μ;
⑶若在竖直平面内对小球施加一个垂直于轻杆方向的恒力F,小球从静止释放后,将以大小为1m/s2的加速度向下运动,则恒力F大小为多大?
⑴PG=24W;⑵μ=0.5;⑶若F垂直于杆向下,F=4N,若F垂直于杆向上,F=36N
【解析】
试题分析:⑴根据题意可知,小球在整个运动过程中受重力mg、杆的弹力N1和摩擦力f1作用,做匀加速直线运动,重力做的功为:WG=mgLsinθ
在整个过程中重力对它做功的平均功率为: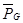 =
=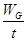 mg
mg sinθ
sinθ
因此小球到达杆底时重力对它做功的功率为:PG=mgvsinθ
根据匀变速直线运动规律可知: =
=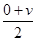
联立以上各式解得:PG=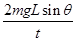 =24W
=24W
⑵根据匀变速直线运动规律可知,小球在下滑过程中的加速度为:a1=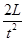
根据牛顿第二定律有:mgsinθ-f1=ma1
在垂直杆方向上有:N1-mgcosθ=0
根据滑动摩擦定律有:f1=μN1
联立以上各式解得:μ=tanθ- =0.5
=0.5
⑶对小球,此时受重力mg、恒力F、杆的弹力N2和滑动摩擦力f2作用,若恒力F垂直于杆向下,则根据牛顿第二定律可知,在垂直于杆方向上有:N2-F-mgcosθ=0
在沿杆向下方向上有:mgsinθ-f2=ma2
根据滑动摩擦定律有:f2=μN2
联立以上三式解得:F= -mgcosθ=4N
-mgcosθ=4N
若恒力F垂直于杆向上,由于a2=1m/s2<a1=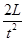 =2m/s2,因此,施加恒力F后,小球所受的摩擦力变大,杆对小球的弹力变大,即N2>N1=mgcosθ
=2m/s2,因此,施加恒力F后,小球所受的摩擦力变大,杆对小球的弹力变大,即N2>N1=mgcosθ
所以此时杆对小球的弹力应垂直于杆向下,在垂直于杆方向上有:F-mgcosθ-N2=0
联立以上各式解得:F= +mgcosθ=36N
+mgcosθ=36N
考点:本题主要考查了匀变速直线运动规律、牛顿第二定律、滑动摩擦定律的应用问题,属于中档题。

 m/s2)求:
m/s2)求:

 =37°时立方体平衡且不动,作用在立方体上的水平推力F1应为多大?
=37°时立方体平衡且不动,作用在立方体上的水平推力F1应为多大?
 。一带正电
。一带正电 的小物块质量为m=0.5kg,它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,试求:(g=10m/s2)
的小物块质量为m=0.5kg,它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,试求:(g=10m/s2)