题目内容
如图所示，光滑圆弧轨道与光滑斜面在B点平滑连接，圆弧半径为R=0.4m，一半径很小、质量为m=0.2kg的小球从光滑斜面上A点由静止释放，恰好通过圆弧轨道最高点D，g取10m/s2。求：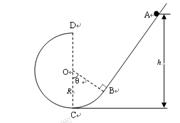
（1）小球最初自由释放位置A离最低点C的高度
；
（2）小球运动到C点时对轨道的压力大小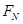
；
（3）若斜面倾斜角与图中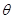
相等，均为53°，小球离开D点至落到斜面上运动了多长时间？
解析试题分析：（1）小球恰好通过最高点D，则有
得
从A点到D点由动能定理（或机械能守恒定律）得：
得
由A到C由动能定理：
得
对C点，有：
得
由牛顿第三定律得，C点对轨道的压力
（3）设撞到斜面上E点离B点的距离为
，飞行时间为t，由平抛运动规律可得
水平方向 
竖直方向 
由上面两式解得 
（
舍去）
所以小球从离开D点至第一次落回到斜面上运动的时间是0.27s．
考点：考查功能关系
点评：本题难度较小，在最低点由支持力和重力的合力提供向心力，分析平抛运动时应明确水平位移和竖直位移
练习册系列答案
学业测评一课一测系列答案
相关题目
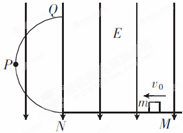（2011?安徽模拟）如图所示，在E=1×103V/m的竖直匀强电场中，有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接，半圆形轨道平面与电场线平行，P为QN圆弧的中点，其半径R=40cm，一带正电q=10-4C的小滑块质量m=10g，与水平轨道间的动摩擦因数μ=0.15，位于N点右侧1.5m处，取g=10m/s2，求：
如图所示是放置在竖直平面内的游戏滑轨，有一质量m=2kg的小球穿在轨道上．滑轨由四部分粗细均匀的滑杆组成：水平直轨道AB；倾斜直轨道CD，长L=6m，与水平面间的夹角θ=370；半径R1=1m的圆弧轨道APC；半径R2=3m的圆弧轨道BQED．直轨道与圆弧轨道相切，切点分别为A、B、D、C，E为最低点．倾斜直轨道CD与小球间的动摩擦因数为μ=5/32，其余部分均为光滑轨道，取g=10m/s2，sin37°=0.6，cos37°=0.8．现让小球从AB的正中央以初速度V0=10m/s开始向左运动，问：
（2011?南昌模拟）如图所示，固定在竖直平面内的光滑圆弧轨ABCD，其A点与圆心等高，D点为轨道最高点．DB为竖直线，AC为水平线，AE为水平面．今使小球自A点正上方某处由静止释放，且从A点进入圆轨道运动，只要适当调节释放点的高度．总能保证小球最终通过最高点D，则小球在通过D点后（ ）
（2013?佛山一模）如图所示，倾斜轨道AB的倾角为37°，CD、EF轨道水平，AB与CD通过光滑圆弧管道BC连接，CD右端与竖直光滑圆周轨道相连．小球可以从D进入该轨道，沿轨道内侧运动，从E滑出该轨道进入EF水平轨道．a、b为两完全相同的小球，a球由静止从A点释放，在C处与b球发生弹性碰撞．已知AB长为5R，CD长为R，重力加速度为g，小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5，sin37°=0.6，cos37°=0.8，圆弧管道BC入口B与出口C的高度差为1.8R．求：
如图所示，倾斜粗糙轨道AB的倾角为37°，CD、EF轨道水平，AB与CD通过光滑圆弧管道BC连接，CD右端与竖直光滑圆周轨道相连，小球可以从D进入该轨道，沿圆轨道内侧运动．小球从A点静止释放，已知AB长为5R，光滑水平轨道CD足够长，圆弧管道BC入口B与出口C的高度差为1.5R，小球与斜轨AB间的动摩擦因数为0.5，重力加速度为g，sin37°=0.6，cos37°=0.8．求：