题目内容
2. 如图所示,坐标平面的第Ⅰ象限内存在大小为E2=$\frac{2mg}{q}$、方向竖直向下的匀强磁场,足够长的薄挡板MN垂直x轴放置且离原点O的距离为L,第Ⅱ象限内存在垂直于纸面向里的匀强磁场B和竖直向下的匀强电场E1=$\frac{1}{2}$E2(E1、E2未矢).一质量为m,带电量为-q的小球(可视为质点),自A点(-d,0)以一定的速度垂直于x轴进入磁场,恰好到达O点.(已知重力加速度为g)求:
如图所示,坐标平面的第Ⅰ象限内存在大小为E2=$\frac{2mg}{q}$、方向竖直向下的匀强磁场,足够长的薄挡板MN垂直x轴放置且离原点O的距离为L,第Ⅱ象限内存在垂直于纸面向里的匀强磁场B和竖直向下的匀强电场E1=$\frac{1}{2}$E2(E1、E2未矢).一质量为m,带电量为-q的小球(可视为质点),自A点(-d,0)以一定的速度垂直于x轴进入磁场,恰好到达O点.(已知重力加速度为g)求:(1)小球从A点进入磁场时,速度V的大小;
(2)若小球现仍从A点进入磁场但初速度大小为原来的4倍,为使小球平行于x轴进入第一象限,求小球速度方向与x轴正向间的夹角θ大小;
(3)在满足(2)问情况下,小球打到挡板上时的纵坐标y.
分析 (1)小球在第Ⅱ象限内受到的重力与电场力平衡,恰好做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律和几何知识结合解答.
(2)粒子初速度为原来的4倍时半径为r1,速度为v1,根据牛顿第二定律求得r1.为使小球平行于x轴进入电场,圆心O在y轴上,由几何知识求出速度方向与x轴正方向的夹角,再画出轨迹.
(3)在第Ⅰ象限内小球做类平抛运动,由牛顿第二定律求出加速度.由两个分位移公式求出y.
解答 解:(1)在第Ⅱ象限内,因为qE1=mg,则小球在第Ⅱ象限中做匀速圆周运动,设轨迹半径为r,速度为v,据匀速圆周运动的规律得:
qvB=m$\frac{{v}^{2}}{r}$…①
又 r=$\frac{d}{2}$…②
联立解得:v=$\frac{qBd}{2m}$
(2)粒子初速度为原来的4倍时半径为r1,速度为v1,据匀速圆周运动的规律得:
qv1B=m$\frac{{v}_{1}^{2}}{{r}_{1}}$…③
v1=4v0…④
联立①②③④解得:r1=2d,v1=$\frac{2qBd}{m}$…⑤
为使小球平行于x轴进入电场,圆心O在y轴上,设速度方向与x轴正方向的夹角为θ,由几何关系知:
sinθ=$\frac{OA}{O′A}$=$\frac{l}{2L}$=0.5,
则θ=30°或θ=150°,如右图所示.
(3)在第Ⅰ象限内小球的加速度 a=$\frac{q{E}_{1}-mg}{m}$=g…⑥
方向竖直向上,小球做类平抛运动,在第Ⅰ象限内小球的竖直方向偏移量 y1=$\frac{1}{2}a{t}^{2}$…⑦
水平方向 L=v1t…⑧
由⑤⑥⑦⑧解得:y1=$\frac{{m}^{2}{L}^{2}g}{8{q}^{2}{B}^{2}{d}^{2}}$
在两种情况下,有:y=(2±$\sqrt{3}$)d+$\frac{{m}^{2}{L}^{2}g}{8{q}^{2}{B}^{2}{d}^{2}}$.
答:(1)小球从A点进入磁场时,速度V的大小是$\frac{qBd}{2m}$.
(2)为使小球平行于x轴进入电场,速度方向与x轴正方向的夹角为θ=30°或θ=150°.
(3)小球打到挡板上时的纵坐标y是(2±$\sqrt{3}$)d+$\frac{{m}^{2}{L}^{2}g}{8{q}^{2}{B}^{2}{d}^{2}}$.
点评 本题是带电粒子在复合场中运动的问题,关键要正确分析粒子的受力情况,判断其运动情况,运用力学的基本规律:牛顿第二定律、运动学公式及几何知识结合解答.

 阅读快车系列答案
阅读快车系列答案 如图所示,左边是一个原先不带电的导体,右边C是后来靠近导体的带正电金属球,若用绝缘工具沿图示某条虚线将导体切开,分导体为A、B两部分,这两部分所带电荷量的数值分别为QA、QB,则下列结论正确的是( )
如图所示,左边是一个原先不带电的导体,右边C是后来靠近导体的带正电金属球,若用绝缘工具沿图示某条虚线将导体切开,分导体为A、B两部分,这两部分所带电荷量的数值分别为QA、QB,则下列结论正确的是( )| A. | 沿虚线d切开,A带负电,B带正电,且QA>QB | |
| B. | 只有沿虚线b切开,才有A带正电,B带负电,且QA=QB | |
| C. | 沿虚线a切开,A带正电,B带负电,且QA<QB | |
| D. | 沿任意一条虚线切开,都有A带正电,B带负电,而QA、QB的值与所切的位置有关 |
 均匀的长杆斜靠在光滑的竖直墙上,当杆与墙成θ=37°时杆平衡状态,则地面与杆间的动摩擦因数应满足(tanθ=$\frac{3}{4}$)( )
均匀的长杆斜靠在光滑的竖直墙上,当杆与墙成θ=37°时杆平衡状态,则地面与杆间的动摩擦因数应满足(tanθ=$\frac{3}{4}$)( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{4}{5}$ |
| A. | 两物体质量相同 | B. | 两物体体积相同 | ||
| C. | 两物体摩尔质量相同 | D. | 两物体摩尔数相同 |
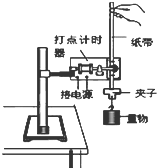 用如图所示的实验装置验证机械能守恒定律.实验所用电源为学生电源,输出电压为6V的交流电和直流电两种.重锤从高处由静止开始下落,重锤上拖着的纸带打出一系列的点,对纸带上的点痕进行测量,据此验证机械能守恒定律.
用如图所示的实验装置验证机械能守恒定律.实验所用电源为学生电源,输出电压为6V的交流电和直流电两种.重锤从高处由静止开始下落,重锤上拖着的纸带打出一系列的点,对纸带上的点痕进行测量,据此验证机械能守恒定律.



 如图所示,在坐标系xOy内有一半径为R的圆形匀强磁场区域,圆心O1坐标为(0,R),方向垂直纸面向外.在虚线x=R的右侧区域内,有一场强大小为E,沿y轴负方向的匀强电场.一质量为m、电荷量为q的带正电的粒子,以速度v0从O点垂直于磁场方向射入圆形磁场区域,不计粒子重力,粒子运动轨迹在xOy平面内.
如图所示,在坐标系xOy内有一半径为R的圆形匀强磁场区域,圆心O1坐标为(0,R),方向垂直纸面向外.在虚线x=R的右侧区域内,有一场强大小为E,沿y轴负方向的匀强电场.一质量为m、电荷量为q的带正电的粒子,以速度v0从O点垂直于磁场方向射入圆形磁场区域,不计粒子重力,粒子运动轨迹在xOy平面内.