��Ŀ����
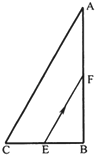
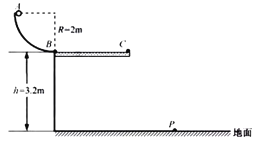
����Ŀ����ͼ��ʾ��һ����ɰ뾶Ϊ2 m���ķ�֮һ��ֱԲ�����AB�ͳ��ȿ��Ե��ڵ�ˮƽֱ���BC��B��ƽ�����Ӷ��ɡ�����һ����Ϊ0.2 kg��С���A�����ٶ��ͷţ�����Բ���ϵ�B��ʱ����������ù������ѹ����СΪ3.6 N��С��BC����������Ϊ��������0.2����Ȼ���C��ˮƽ���������䵽ˮƽ���ϵ�P�㣬P��C�����ĸ߶Ȳ�Ϊ3.2 m��С���˶������п�����Ϊ�ʵ㣬�Ҳ��ƿ���������
��1����С���˶���B����ٶȴ�С��
��2����С����Բ������Ͽ˷�Ħ���������Ĺ���
��3��ΪʹС�����P��B���ˮƽ���������BC�εij��ȣ�
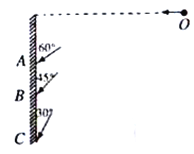
��4��С���䵽P��������������ײ��ֹ������С��ÿ����ײ��е����ʧ75%����ײǰ���ٶȷ��������ļн���ȡ���С���C��ɳ���ֹ�����ʱ�䡣
���𰸡���1��4m/s��2��2.4J��3��3.36m��4��2.4s
�������������������1��С����B���ܵ���������֧�����ĺ����ṩ���������ɴ˼������B����ٶȣ���2�����ݶ��ܶ����������С����Բ������Ͽ˷�Ħ���������Ĺ�����3�����ƽ���˶��Ĺ�ʽ���������ΪʹС�����P��B���ˮƽ�������ʱBC�εij��ȣ���4���ɻ�е�ܵ���ʧ����ٶȵ���ʧ��Ȼ������ֱ�����˶��Ĺ�ʽ�������ʱ�䣬�����ͼ��ɣ�
��1��С����B���ܵ���������֧�����ĺ����ṩ����������![]()
�������ݿɵã�![]()
��2��A��B�Ĺ������������������������ɶ��ܶ����ɵã�![]()
�������ݵã�![]()
��3��B��C�Ĺ����У��ɶ��ܶ����ã�![]()
��ã�![]()
��C�㵽��ص�ʱ�䣺![]()
B��P��ˮƽ���룺![]()
�������ݣ������������ɵã�![]()
��֪����![]() ʱ��P��B��ˮƽ�������ΪL=3.36m
ʱ��P��B��ˮƽ�������ΪL=3.36m
��4������С��ÿ����ײ��е����ʧ75%����![]() ������ײ����ٶ�Ϊ��ײǰ�ٶȵ�
������ײ����ٶ�Ϊ��ײǰ�ٶȵ�![]() ����ײǰ���ٶȷ��������ļн���ȣ�����ײ����ֱ����ķ��ٶ�Ϊ��ײǰ��ֱ������ٶȵ�
����ײǰ���ٶȷ��������ļн���ȣ�����ײ����ֱ����ķ��ٶ�Ϊ��ײǰ��ֱ������ٶȵ�![]() �����Ե�һ����ײ����������ߵ��ʱ����ڴ�C�㵽��ص�ʱ���
�����Ե�һ����ײ����������ߵ��ʱ����ڴ�C�㵽��ص�ʱ���![]() �����Դӵ�һ����ײ�����ڶ�����ײ��ʱ�䣺
�����Դӵ�һ����ײ�����ڶ�����ײ��ʱ�䣺![]() ��ͬ�����ӵڶ�����ײ������������ײ��ʱ�䣺
��ͬ�����ӵڶ�����ײ������������ײ��ʱ�䣺![]() ���ɴ����ƿ�֪���ӵ�n����ײ������n+1����ײ��ʱ�䣺
���ɴ����ƿ�֪���ӵ�n����ײ������n+1����ײ��ʱ�䣺![]()
С���˶�����ʱ�䣺![]()
����ѧ���ɷ��ֿɵã�![]()