题目内容
（14分）
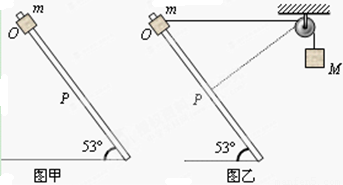
有一个固定的光滑直杆，该直杆与水平面的夹角为53°，杆上套着一个质量为m=2kg的滑块(可视为质点)。
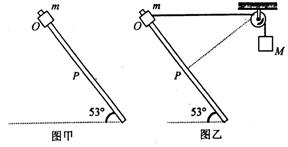
（1）如图甲所示，滑块从O点由静止释放，下滑了位移x=1m后到达P点，求滑块此时的速率。
（2）如果用不可伸长的细绳将滑块m与另一个质量为M=2.7kg的物块通过光滑的定滑轮相连接，细绳因悬挂M而绷紧，此时滑轮左侧绳恰好水平，其长度l =
m（如图乙所示）。再次将滑块从O点由静止释放，求滑块滑至P点的速度大小。
（整个运动过程中M不会触地，sin53°＝0.8，cos53°＝0.6，g取10m/s2）
 |
（14分）
（1）设滑块下滑至P点时的速度为v1,由机械能守恒定律得
mgxsin53º=
①（3分）
解得 v1=4m/s ②（2分）
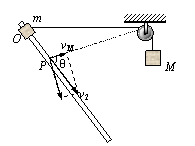
（2）设滑块再次滑到P点时速度为v2，绳与斜杆的夹角为θ，
M的速度为vM，如图将绳端进行分解得：
vM= v2cosθ
由几何关系得θ=90 º ③（2分）
vM=0 ④（2分）
再由系统机械能守恒定律得：
Mgl(1－sin53º)+mgxsin53º=
mv22+0 ⑤（3分）
解得 v2=5 m/s ⑥（2分）
 |
练习册系列答案
相关题目
有一个固定的光滑直杆与水平面的夹角为 53°，杆上套着一个质量为 m=2kg 的滑块（可视为质点）．用不可伸长的细绳将滑块 m 与另一个质量为 M=2.7kg 的物块通过光滑的定滑轮相连接，细绳因悬挂 M 而绷紧，此时滑轮左侧细绳恰好水平，其长度 L=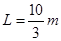
，p点与滑轮的连线与直杆垂直（如图所示）．现将滑块m从图中O点由静止释放，（整个运动过程中M不会触地,g=10m/s2）。则滑块m滑至P点时的速度大小为（ ）
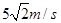
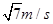
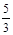m（如图乙所示）。再次将滑块从O点由静止释放，求滑块滑至P点的速度大小。（整个运动过程中M不会触地，sin53°＝0.8，cos53°＝0.6，g取10m/s2）
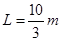，p点与滑轮的连线与直杆垂直（如图所示）．现将滑块m从图中O点由静止释放，（整个运动过程中M不会触地,g=10m/s2）。则滑块m滑至P点时的速度大小为（ ）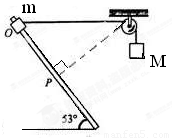
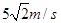B．5m/s 
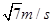D．2m/s
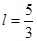m（如图乙所示）．再次将滑块从O点由静止释放，求滑块滑至P点的速度大小。
）