题目内容
16.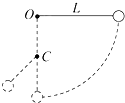 小球m用长为L的悬线固定在O点,在O点正下方有一光滑圆钉C(如图所示).今把小球拉到悬线呈水平后无初速地释放,当悬线呈竖直状态且与钉相碰时( )
小球m用长为L的悬线固定在O点,在O点正下方有一光滑圆钉C(如图所示).今把小球拉到悬线呈水平后无初速地释放,当悬线呈竖直状态且与钉相碰时( )| A. | 小球的角速度突然增大 | |
| B. | 小球的向心加速度突然增大 | |
| C. | 钉子的位置越靠近小球,线就越容易断 | |
| D. | 钉子的位置越远离小球,线就越容易断 |
分析 由机械能守恒可知小球到达最低点的速度,小球碰到钉子后仍做圆周运动,由向心力公式可得出绳子的拉力与小球转动半径的关系;由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系.
解答 解:A、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,而半径变小,则$ω=\frac{v}{r}$变大,故A正确;
B、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,但圆周运动的半径减小,向心加速度$a=\frac{{v}^{2}}{R}$变大,故B正确;
C、根据牛顿第二定律,有:F-mg=m$\frac{{v}^{2}}{R}$,故绳子的拉力F=mg+m$\frac{{v}^{2}}{R}$,
钉子的位置越靠近小球,半径越小,绳子拉力越大,绳子越容易断,故C正确,D错误.
故选:ABC
点评 本题中要注意细绳碰到钉子前后转动半径的变化,再由向心力公式分析绳子上的拉力变化.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
7. 木块a和b用一根轻弹簧连接起来,放在光滑水平面上,a紧靠在墙壁上,在b上施加向左的水平力使弹簧压缩,如图所示,当撤去外力后,下列说法中正确的是( )
木块a和b用一根轻弹簧连接起来,放在光滑水平面上,a紧靠在墙壁上,在b上施加向左的水平力使弹簧压缩,如图所示,当撤去外力后,下列说法中正确的是( )
 木块a和b用一根轻弹簧连接起来,放在光滑水平面上,a紧靠在墙壁上,在b上施加向左的水平力使弹簧压缩,如图所示,当撤去外力后,下列说法中正确的是( )
木块a和b用一根轻弹簧连接起来,放在光滑水平面上,a紧靠在墙壁上,在b上施加向左的水平力使弹簧压缩,如图所示,当撤去外力后,下列说法中正确的是( )| A. | a尚未离开墙壁前,a和b系统的动量守恒,机械能守恒 | |
| B. | a尚未离开墙壁前,a与b系统的动量不守恒,机械能不守恒 | |
| C. | a离开墙后,a、b系统动量守恒,机械能守恒 | |
| D. | a离开墙后,a、b系统动量守恒,机械能不守恒 |
4. 如图所示,木箱内有一竖直放置的弹簧,弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块压在箱顶上,若在某一段时间内,物块对箱顶刚好无压力,则在此段时间内木箱的运动状态可能为( )
如图所示,木箱内有一竖直放置的弹簧,弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块压在箱顶上,若在某一段时间内,物块对箱顶刚好无压力,则在此段时间内木箱的运动状态可能为( )
 如图所示,木箱内有一竖直放置的弹簧,弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块压在箱顶上,若在某一段时间内,物块对箱顶刚好无压力,则在此段时间内木箱的运动状态可能为( )
如图所示,木箱内有一竖直放置的弹簧,弹簧上方有一物块,木箱静止时弹簧处于压缩状态且物块压在箱顶上,若在某一段时间内,物块对箱顶刚好无压力,则在此段时间内木箱的运动状态可能为( )| A. | 加速下降 | B. | 加速上升 | C. | 减速上升 | D. | 匀速下降 |
11.下列关于波的衍射的说法正确的是( )
| A. | 衍射是一切机械波特有的现象 | |
| B. | 只有缝或孔(障碍物)的尺寸跟波长相差不多,或者比波长更小时,才能发生衍射现象 | |
| C. | 对同一列波,缝或孔(障碍物)越小,衍射现象越明显 | |
| D. | 声波容易发生衍射是由于声波波长较大 |
1. 某投掷游戏可简化为如图所示的物理模型,投掷者从斜面底端A正上方的某处将一小球以速度v0水平抛出,小球飞行一段时间后撞在斜面上的P点,该过程水平射程为x,飞行时间为t,有关该小球运动过程中两个物理量之间的图象关系如a、b、c所示,不计空气阻力的影响,下面叙述不正确的是( )
某投掷游戏可简化为如图所示的物理模型,投掷者从斜面底端A正上方的某处将一小球以速度v0水平抛出,小球飞行一段时间后撞在斜面上的P点,该过程水平射程为x,飞行时间为t,有关该小球运动过程中两个物理量之间的图象关系如a、b、c所示,不计空气阻力的影响,下面叙述不正确的是( )
 某投掷游戏可简化为如图所示的物理模型,投掷者从斜面底端A正上方的某处将一小球以速度v0水平抛出,小球飞行一段时间后撞在斜面上的P点,该过程水平射程为x,飞行时间为t,有关该小球运动过程中两个物理量之间的图象关系如a、b、c所示,不计空气阻力的影响,下面叙述不正确的是( )
某投掷游戏可简化为如图所示的物理模型,投掷者从斜面底端A正上方的某处将一小球以速度v0水平抛出,小球飞行一段时间后撞在斜面上的P点,该过程水平射程为x,飞行时间为t,有关该小球运动过程中两个物理量之间的图象关系如a、b、c所示,不计空气阻力的影响,下面叙述不正确的是( )| A. | 直线a是小球的竖直分速度随离地高度变化的关系 | |
| B. | 曲线b可能是小球的竖直分速度随下落高度变化的关系 | |
| C. | 直线c是飞行时间t随初速度v0变化的关系 | |
| D. | 直线c也可以是水平射程x随初速度v0变化的关系 |
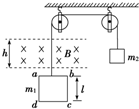 如图所示,线圈abcd每边长l=0.20m,线圈质量m1=0.10kg、电阻R=0.10Ω,砝码质量m2=0.14kg.线圈上方的匀强磁场磁感应强度B=0.5T,方向垂直线圈平面向里,磁场区域的宽度为h=l=0.20m.砝码从某一位置下降,使ab边进入磁场开始做匀速运动.求:
如图所示,线圈abcd每边长l=0.20m,线圈质量m1=0.10kg、电阻R=0.10Ω,砝码质量m2=0.14kg.线圈上方的匀强磁场磁感应强度B=0.5T,方向垂直线圈平面向里,磁场区域的宽度为h=l=0.20m.砝码从某一位置下降,使ab边进入磁场开始做匀速运动.求: 如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,用这些光照射逸出功为2.49eV的金属钠,则这群氢原子能发出3种频率不同的光,其中从n=3能级跃迁到n=1能级所发出的光波长最最短,金属钠表面所发出的光电子的初动能最大值为9.60eV.
如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,用这些光照射逸出功为2.49eV的金属钠,则这群氢原子能发出3种频率不同的光,其中从n=3能级跃迁到n=1能级所发出的光波长最最短,金属钠表面所发出的光电子的初动能最大值为9.60eV.