题目内容
如图所示,两个完全相同的小球A、B用等长的细线悬于O点.线长L.若将A由图示位置静止释放,则B球被碰后第一次速度为零时的高度不可能是 ( )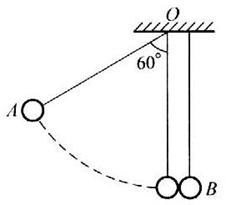
A.L/2 B.L/4 C.L/8 D.L/10
D
解析试题分析:小球A从释放到最低点,由动能定理可知: ,解得:
,解得: .若A与B发生完全弹性碰撞,由能量守恒定律和动量守恒定律可知两者交换速度,即
.若A与B发生完全弹性碰撞,由能量守恒定律和动量守恒定律可知两者交换速度,即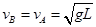 ,B上升过程中由动能定理可知:
,B上升过程中由动能定理可知: ,解得:
,解得: ;若A与B发生完全非弹性碰撞即AB粘在一起,由动量守恒定律可知:
;若A与B发生完全非弹性碰撞即AB粘在一起,由动量守恒定律可知: ,解得:
,解得: ,在AB上升过程中,由动能定理可知:
,在AB上升过程中,由动能定理可知: ,解得:
,解得: ,所以B球上升的高度
,所以B球上升的高度 ,故选项D错误.
,故选项D错误.
考点:考查动量守恒定律和动能定理在碰撞中的应用,关键在于根据两球碰撞的可能情况解出高度的范围.

 阅读快车系列答案
阅读快车系列答案一质量为2kg的滑块,以4m/s的速度在光滑水平面上向左滑行,从某一时刻起,在滑块上作用一向右的水平力,经过一段时间,滑块的速度方向变为向右,大小为4m/s,在这段时间里水平力所做的功为 ( )
| A.32J | B.8J | C.16J | D.0 |
如图所示,半圆形轨道MON竖直放置且固定在地面上,直径MN是水平的。一小物块从M点正上方高度为H处自由下落,正好在M点滑入半圆轨道,测得其第一次离开N点后上升的最大高度为 。小物块接着下落从N点滑入半圆轨道,在向M点滑行过程中(整个过程不计空气阻力)
。小物块接着下落从N点滑入半圆轨道,在向M点滑行过程中(整个过程不计空气阻力)
| A.小物块正好能到达M点 | B.小物块一定到不了M点 |
| C.小物块一定能冲出M点 | D.不能确定小物块能否冲出M点 |
如图,x轴在水平地面上,y轴竖直向上,在y轴上的P点分别沿x轴正方向和y轴正方向以相同大小的初速度抛出两个小球a和b,轨迹如图,不计空气阻力,若b上行的最大高度等于P点离地的高度,则从抛出到落地,有( )
A.a的运动时间是b的运动时间的( )倍 )倍 |
B.a的位移大小是b的位移大小的 倍 倍 |
| C.a、b落地时的速度相同,因此动能一定相同 |
| D.a、b落地时的速度不同,但动能一定相同 |
如图所示,在粗糙的斜面上固定一点电荷Q,在M点无初速度释放带有恒定电荷的小物块,小物块在Q的电场中沿斜面运动到N点停下。则从M到N的过程中,下列说法正确的是( )
| A.小物块所受的电场力减小 |
| B.小物块的电势能减小 |
| C.M点的电势一定低于N点的电势 |
| D.小物块电势能变化量的大小一定小于克服摩擦力做的功 |
如图所示,在倾角θ=30o的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球A和B,两球之间用一根长L=0.2m的轻杆相连,小球B距水平面的高度h=0.1m。两球从静止开始下滑到光滑地面上,不计球与地面碰撞时的机械能损失,g取10m/s2。则下列说法中正确的是:( )
| A.下滑的整个过程中A球机械能守恒 |
| B.下滑的整个过程中两球组成的系统机械能守恒 |
| C.两球在光滑水平面上运动时的速度大小为2 m/s |
D.系统下滑的整个过程中B球机械能的增加量为 J J |
如图所示,一个质量为m的物体(可视为质点),由斜面底端的A点以某一初速度冲上倾角为300的固定斜面做匀减速直线运动,减速的加速度大小为g,物体沿斜面上升的最大高度为h,在此过程中
| A.重力势能增加了2mgh | B.机械能损失了mgh |
| C.动能损失了mgh | D.系统生热 |
如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点。下列说法中正确的是( )
| A.小球从A出发到返回A的过程中,位移为零,外力做功为零 |
| B.小球从A上升到C与从C上升到B的过程,减少的动能相等 |
| C.小球从A上升到C与从C上升到B的过程,速度的变化率相等 |
| D.小球从A上升到C与从C上升到B的过程,损失的机械能相等 |
如图所示,水平向左的匀强电场场强大小为E,一根不可伸长的绝缘细线长度为l,细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后由静止释放,小球沿弧线运动到细线与水平方向夹角θ=60°的位置B时速度为零.以下说法中正确的是( )
| A.A点电势低于B点电势 |
B.小球受到的电场力与重力的关系是Eq= mg mg |
| C.小球在B点时,细线拉力为2mg |
D.小球从A运动到B过程中,电场力对其做的功为 Eql Eql |