题目内容
19. 如图为一列沿x轴传播的简谐横波在t1=0(图中实线所示)以及在t2=0.02s(虚线所示)两个时刻的波形图象.
如图为一列沿x轴传播的简谐横波在t1=0(图中实线所示)以及在t2=0.02s(虚线所示)两个时刻的波形图象.(1)若t2-t1<$\frac{T}{2}$(T为该波的周期)求波的传播方向、传播速度和波的周期,并画出这列波在0.2s时刻的波形图;
(2)若t2-t1>$\frac{T}{2}$,求这列波的波速.
分析 (1)由图可以读出横波的波长.波的一个周期内传播的距离是λ,当t2-t1<$\frac{1}{2}$T时,可知波传播的距离s不到一个波长,求出波传播的距离,再求解波速.运用波形平移法画出0.2s时刻的波形图.
(2)若t2-t1>$\frac{T}{2}$,结合波的周期性求出波传播的距离,再求波速.
解答 解:(1)由于当t2-t1<$\frac{1}{2}$T时,波沿x轴正向传播,波传播的距离为△x=2m
波速v=$\frac{△x}{△t}$=$\frac{2}{0.02}$=100m/s
周期 T=$\frac{λ}{v}$=$\frac{16}{100}$s=0.16s
因为 t=0.2s=T+$\frac{T}{4}$,则这列波在0.2s时刻的波形图如下. 
(2)若t2-t1>$\frac{T}{2}$,波沿x轴负向传播
传播的距离可能为△x右=(n+1)λ+2m,(n=0,1,2…)
波速 v右=$\frac{△{x}_{右}}{△t}$=[800(n+1)+100]m/s,(n=0,1,2…)
若波向左传,传播的距离可能为△x左=nλ+14m,(n=0,1,2…)
波速 v左=$\frac{△{x}_{左}}{△t}$=[800n+700]m/s,(n=0,1,2…)
答:(1)若t2-t1<$\frac{T}{2}$(T为该波的周期),波沿x轴正向传播、传播速度是100m/s,波的周期是0.16s,画出这列波在0.2s时刻的波形图如图;
(2)若t2-t1>$\frac{T}{2}$,这列波的波速是:[800(n+1)+100]m/s,(n=0,1,2…)或[800n+700]m/s,(n=0,1,2…).
点评 本波是典型的多解问题.要注意波的周期性和双向性,运用波形的平移法进行分析和求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( )
如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( )| A. | 若v一定,θ越大,则粒子离开磁场的位置距O点越远 | |
| B. | 若v一定,θ越大,则粒子在磁场中运动的时间越短 | |
| C. | 若θ一定,v越大,则粒子在磁场中运动的角速度越大 | |
| D. | 若θ一定,v越大,则粒子在磁场中运动的时间越短 |
| A. | 引力常量是两个质量为1kg的物体相距1m时的相互吸引力 | |
| B. | 牛顿发现万有引力定律时,给出了引力常量的值 | |
| C. | 引力常量的测定,证明了万有引力的存在 | |
| D. | 引力常量G是不变的,其数值大小与单位制的选择无关 |
| A. | 上升到最高点过程重力势能增加了20J | |
| B. | 从最高点回到A点过程克服阻力做功4J | |
| C. | 上升到最高点过程机械能减少了8J | |
| D. | 从最高点回到A点过程重力势能减少了12J |
 如图所示,灯泡A、B与固定电阻的阻值均为R,L是带铁芯的理想线圈,电源的内阻不计.开关S1、S2均闭合且电路达到稳定.已知电路中的各种元件均在安全范围之内.下列判断中正确的是( )
如图所示,灯泡A、B与固定电阻的阻值均为R,L是带铁芯的理想线圈,电源的内阻不计.开关S1、S2均闭合且电路达到稳定.已知电路中的各种元件均在安全范围之内.下列判断中正确的是( )| A. | 灯泡A中有电流通过,方向为a→b | |
| B. | 将S1断开的瞬间,灯泡A、B同时熄灭 | |
| C. | 将S1断开的瞬间,通过灯泡A的电流最大值要比原来通过灯泡B的电流大 | |
| D. | 将S2断开,电路达到稳定,灯泡A、B的亮度相同 |
| A. | 气体的密度增大 | B. | 气体的压强增大 | ||
| C. | 气体分子的平均动能减小 | D. | 气体分子的平均动能增大 |
 竖直悬挂的弹簧振子下端装有记录笔,在竖直面内放置记录纸.当振子上下振动时,以水平向左速度v=10m/s匀速拉动记录纸,记录笔在纸上留下记录的痕迹,建立坐标系,测得的数据如图所示,振子振动的振幅为0.05m,频率为10Hz.
竖直悬挂的弹簧振子下端装有记录笔,在竖直面内放置记录纸.当振子上下振动时,以水平向左速度v=10m/s匀速拉动记录纸,记录笔在纸上留下记录的痕迹,建立坐标系,测得的数据如图所示,振子振动的振幅为0.05m,频率为10Hz.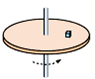 如图所示,一个水平匀质圆盘绕垂直于盘面的固定对称轴匀速转动,角速度是4rad/s,盘面上离转轴距离0.1m处有一质量为0.1kg的小物体能随盘一起转动.求:
如图所示,一个水平匀质圆盘绕垂直于盘面的固定对称轴匀速转动,角速度是4rad/s,盘面上离转轴距离0.1m处有一质量为0.1kg的小物体能随盘一起转动.求: