题目内容
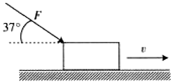
如图所示,光滑水平面上放着长L=2m,质量为M=4.5kg的木板(厚度不计),一个质量为m=1kg的小物体放在木板的最右端,m和M之间的动摩擦因数μ=0.1,开始均静止.今对木板施加一水平向右的恒定拉力F,(g取10m/s2)求:
(1)为使小物体不从木板上掉下,F不能超过多少.
(2)如果拉力F=10N,小物体能获得的最大速度.

(1)为使小物体不从木板上掉下,F不能超过多少.
(2)如果拉力F=10N,小物体能获得的最大速度.

(1)物块随木板运动的最大加速度为a
对小物体由牛顿第二定律:umg=ma
对整体由牛顿第二定律得:Fm=(M+m)a
解得:Fm=5.5N
(2)因施加的拉力F>5.5N,故物块相对木板相对滑动,木板对地运动的加速度为a1,
对木板由牛顿第二定律:F-umg=Ma1
物块在木板上相对运动的时间为t,L=
a1t2-
at2
解得:t=2s
物块脱离木板时的速度最大,vm=at=2m/s
答:(1)为使小物体不从木板上掉下,F不能超过5.5N.
(2)小物体能获得的最大速度为2m/s.
对小物体由牛顿第二定律:umg=ma
对整体由牛顿第二定律得:Fm=(M+m)a
解得:Fm=5.5N
(2)因施加的拉力F>5.5N,故物块相对木板相对滑动,木板对地运动的加速度为a1,
对木板由牛顿第二定律:F-umg=Ma1
物块在木板上相对运动的时间为t,L=
| 1 |
| 2 |
| 1 |
| 2 |
解得:t=2s
物块脱离木板时的速度最大,vm=at=2m/s
答:(1)为使小物体不从木板上掉下,F不能超过5.5N.
(2)小物体能获得的最大速度为2m/s.

练习册系列答案
相关题目