题目内容
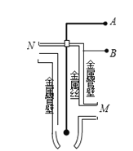
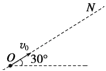
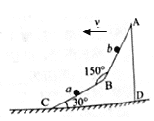
【题目】如图所示,光滑水平面上有一异形滑块ABCD在向左做匀变速运动,竖直平面内存在匀强电场,斜面BC和AB光滑绝缘,上面分别有两个质量均为m的小球a、b相对滑块静止,其中小球b带负电,电荷量大小为q,小球a不带电。重力加速度为g,则下列说法中正确的是
A. 滑块加速度大小为![]()
B. 滑块加速度大小为![]()
C. 电场强度的最小值为![]()
D. 电场强度的最小值为![]()
【答案】C
【解析】
因小球a不带电,以小球a为研究对象进行受力分析,受到重力和支持力作用,根据牛顿第二定律可得mgtao30°=ma,解得a=gtan30°=![]() g,故AB错误;AB斜面与水平方向的夹角为180°-(150°-30°)=60°;对b受力分析如图所示,当电场强度方向沿斜面向上时,场强最小,则:FNcos60°+qEcos30°=mg;FNsin60°-qEminsin30°=ma,解得电场强度最小值Emin=
g,故AB错误;AB斜面与水平方向的夹角为180°-(150°-30°)=60°;对b受力分析如图所示,当电场强度方向沿斜面向上时,场强最小,则:FNcos60°+qEcos30°=mg;FNsin60°-qEminsin30°=ma,解得电场强度最小值Emin=![]() ,故C正确、D错误;故选C。
,故C正确、D错误;故选C。

练习册系列答案
相关题目
【题目】2008年9月25日至28日我国成功实施了“神舟”七号载入航天飞行并实现了航天员首次出舱。飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟。下列判断正确的是( )
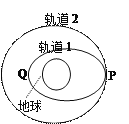
A.飞船变轨前后的机械能相等 |
B.飞船在圆轨道上时航天员出舱前后都处于失重状态 |
C.飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度 |
D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 |