题目内容
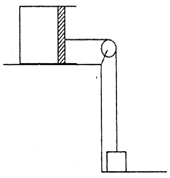
【题目】如图所示，两块相同平板P1，P2置于光滑水平面上，质量均为m．P2的上表面光滑，右端固定一轻质弹簧．物体P置于P1的最右端，质量为2m且可看作质点．P1与P以共同速度v0向右运动，与静止的P2发生碰撞，碰撞时间极短，碰撞后P1与P2粘连在一起，P滑上P2直至将弹簧压缩至最短（弹簧始终在弹性限度内）．求：
（1）P1、P2刚碰完时的共同速度v1；
（2）P1与P2碰撞过程中损失的机械能；
（3）当弹簧被压缩至最短时，P的速度v2；
（4）此过程中弹簧获得的最大弹性势能Epm．
【答案】(1) 
(2) 
(3) 
(4) 
【解析】试题分析：P1、P2碰撞过程动量守恒，由动量守恒定律可以求出碰撞后的速度；由能量守恒定律可以求出损失的机械能；当弹簧压缩最大时，P1、P2、P三者具有共同速度v3，由动量守恒定律可以求出P的速度；由能量守恒定律可以求出弹簧的最大弹性势能。
（1）P1、P2碰撞过程系统动量守恒，以向右为正方向，由动量守恒定律得：mv0=2mv1
解得：
，方向水平向右
（2）由能量守恒定律可知，P1、P2碰撞过程系统损失的机械能：
（3）P1、P2、P系统动量守恒，以向右为正方向，由动量守恒定律得：2mv1+2mv0=4mv2
解得：
，方向水平向右
（4）当弹簧压缩最大时，P1、P2、P三者具有共同速度v2，以向右为正方向，
由动量守恒定律得：mv0+2mv0=4mv2
对系统，由能量守恒定律得：
解得：
练习册系列答案
相关题目
