题目内容
【题目】如图所示，一匀强磁场磁感应强度为B；方向向里，其边界是半径为R的圆，AB为圆的一直径.在A点有一粒子源向圆平面内的各个方向发射质量m、电量-q的粒子，粒子重力不计．
(1)有一带电粒子以
的速度垂直磁场进入圆形区域，恰从B点射出．求此粒子在磁场中运动的时间．
(2)若磁场的边界是绝缘弹性边界(粒子与边界碰撞后将以原速率反弹)，某粒子沿半径方向射入磁场，经过2次碰撞后回到A点，则该粒子的速度为多大?
(3)若R=3cm、B=0.2T，在A点的粒子源向圆平面内的各个方向发射速度均为3×105m／s、比荷为108C／kg的粒子．试用阴影图画出粒子在磁场中能到达的区域，并求出该区域的面积(结果保留2位有效数字)．
【答案】（1）
（2）
（3）
【解析】
（1）根据洛伦兹力提供向心力，求出粒子的半径，通过几何关系得出圆弧所对应的圆心角，根据周期公式，结合t=
T求出粒子在磁场中运动的时间．
（2）粒子径向射入磁场，必定径向反弹，作出粒子的轨迹图，通过几何关系求出粒子的半径，从而通过半径公式求出粒子的速度．
（3）根据粒子的半径公式求出粒子的轨道半径，作出粒子轨迹所能到达的部分，根据几何关系求出面积．
（1）由
得r1=2R
粒子的运动轨迹如图所示，则α＝
因为周期
．
运动时间
．
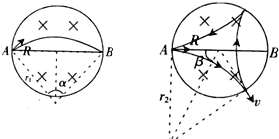
（2）粒子运动情况如图所示，β＝．
r2＝Rtanβ＝
R
由
得
（3）粒子的轨道半径r3＝
＝1.5cm
粒子到达的区域为图中的阴影部分
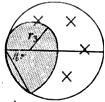
区域面积为S=
πr32+2×
π(2r3)2r32=9.0×10-4m2
练习册系列答案
相关题目
