题目内容
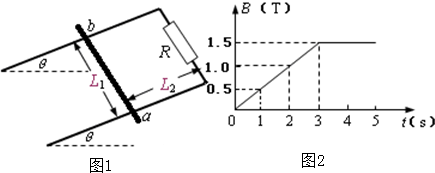
如图甲所示,两根足够长、电阻不计的光滑平行金属导轨相距为L1=1m,导轨平面与水平面成θ=30°角,上端连接阻值R=1.5Ω的电阻;质量为m=0.2kg、阻值r=0.5Ω的金属棒ab放在两导轨上,距离导轨最上端为L2=4m,棒与导轨垂直并保持良好接触.整个装置处于一匀强磁场中,该匀强磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图乙所示.为保持ab棒静止,在棒上施加了一平行于导轨平面的外力F,g=10m/s2求:
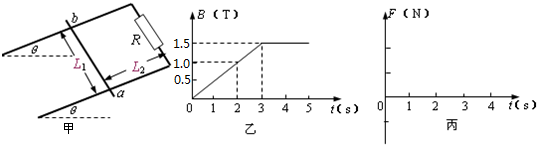
(1)当t=2s时,外力F1的大小;
(2)当t=3s前的瞬间,外力F2的大小和方向;
(3)请在图丙中画出前4s外力F随时间变化的图象(规定F方向沿斜面向上为正);
(4)4s后,撤去外力F,金属棒将由静止开始下滑,这时用电压传感器将R两端的电压即时采集并输入计算机,在显示器显示的电压达到某一恒定值后,记下该时刻棒的位置,测出该位置与棒初始位置相距207.90cm,求棒下滑该距离过程中电阻R上产生的焦耳热.

(1)当t=2s时,外力F1的大小;
(2)当t=3s前的瞬间,外力F2的大小和方向;
(3)请在图丙中画出前4s外力F随时间变化的图象(规定F方向沿斜面向上为正);
(4)4s后,撤去外力F,金属棒将由静止开始下滑,这时用电压传感器将R两端的电压即时采集并输入计算机,在显示器显示的电压达到某一恒定值后,记下该时刻棒的位置,测出该位置与棒初始位置相距207.90cm,求棒下滑该距离过程中电阻R上产生的焦耳热.
分析:(1)由图知,0-3s时间内,B均匀增大,回路中产生恒定的感应电动势和感应电流,根据法拉第电磁感应定律和欧姆定律求出感应电流,由平衡条件求解t=2s时,外力F1的大小.
(2)与上题用同样的方法求出外力F2的大小和方向.
(3)由B-t图象得到B与t的关系式,根据平衡条件得到外力F与t的关系式,再作出图象.
(4)撤去外力后,棒沿导轨向下做变加速运动,最终匀速,当R上电压达到恒定时,棒已做匀速运动,根据平衡条件和安培力与速度的表达式,求出匀速运动的速度,再运用能量守恒定律列式求解整个回路产生的热量Q总.由于R与r串联,电阻R上产生的焦耳热为 QR=
Q总.
(2)与上题用同样的方法求出外力F2的大小和方向.
(3)由B-t图象得到B与t的关系式,根据平衡条件得到外力F与t的关系式,再作出图象.
(4)撤去外力后,棒沿导轨向下做变加速运动,最终匀速,当R上电压达到恒定时,棒已做匀速运动,根据平衡条件和安培力与速度的表达式,求出匀速运动的速度,再运用能量守恒定律列式求解整个回路产生的热量Q总.由于R与r串联,电阻R上产生的焦耳热为 QR=
| R |
| R+r |
解答: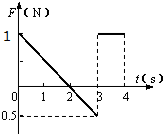 解(1)当t=2s时,回路中产生的感应电动势为:
解(1)当t=2s时,回路中产生的感应电动势为:
E=
L1L2,
B2=1T,应电流为:
I=
=L1L2
=1×4×
A=1A;
根据楞次定律判断可知,ab所受的安培力沿轨道向上;
ab棒保持静止,受力平衡,设外力沿轨道向上,则由平衡条件有:
mgsin30°-B2IL1-F1=0
可解得:F1=mgsin30°-B2IL1=0.2×10×sin30°-1×1×1=0
(2)当t=3s前的瞬间,由图可知,B3=1.5T,设此时外力沿轨道向上,则根据平衡条件得:
F2+B3IL1-mg sin30°=0
则得:F2=mg sin30°-B3IL1=0.2×10×sin30°-1.5×1×1=-0.5N,负号说明外力沿斜面向下.
(3)规定F方向沿斜面向上为正,在0-3s内,根据平衡条件有:
mgsin30°-BIL1-F=0
而B=0.5t(T)
则得:F=mgsin30°-BIL1=0.2×10×sin30°-0.5T×1×1=1-0.5T(N)
当t=0时刻,F=1N.
在3-4s内,B不变,没有感应电流产生,ab不受安培力,则由平衡条件得:F=mgsin30°=0.2×10×sin30°N=1N
画出前4s外力F随时间变化的图象如图所示.
(4)撤去外力后,棒沿导轨向下做变加速运动,最终匀速.当R上电压达到恒定时,棒已做匀速运动.由a=0得:
mgsinθ=B3IL1
又根据闭合欧姆定律得:I=
所以有:vm=
=
m/s=
m/s
该过程中,根据能量守恒定律得:Q总=mgxsinθ-
mv2
而 Q总=QR+Qr
=
故 QR=
Q总
代入数据得:QR=1.5J
答:(1)当t=2s时,外力F1的大小是0;
(2)当t=3s前的瞬间,外力F2的大小是0.5N,方向沿斜面向下;
(3)画出前4s外力F随时间变化的图象如图所示.
(4)棒下滑该距离过程中电阻R上产生的焦耳热是1.5J.
 解(1)当t=2s时,回路中产生的感应电动势为:
解(1)当t=2s时,回路中产生的感应电动势为:E=
| △B |
| △t |
B2=1T,应电流为:
I=
| E |
| R+r |
| △B |
| △t(R+r) |
| 1.5 |
| 3×(1.5+0.5) |
根据楞次定律判断可知,ab所受的安培力沿轨道向上;
ab棒保持静止,受力平衡,设外力沿轨道向上,则由平衡条件有:
mgsin30°-B2IL1-F1=0
可解得:F1=mgsin30°-B2IL1=0.2×10×sin30°-1×1×1=0
(2)当t=3s前的瞬间,由图可知,B3=1.5T,设此时外力沿轨道向上,则根据平衡条件得:
F2+B3IL1-mg sin30°=0
则得:F2=mg sin30°-B3IL1=0.2×10×sin30°-1.5×1×1=-0.5N,负号说明外力沿斜面向下.
(3)规定F方向沿斜面向上为正,在0-3s内,根据平衡条件有:
mgsin30°-BIL1-F=0
而B=0.5t(T)
则得:F=mgsin30°-BIL1=0.2×10×sin30°-0.5T×1×1=1-0.5T(N)
当t=0时刻,F=1N.
在3-4s内,B不变,没有感应电流产生,ab不受安培力,则由平衡条件得:F=mgsin30°=0.2×10×sin30°N=1N
画出前4s外力F随时间变化的图象如图所示.
(4)撤去外力后,棒沿导轨向下做变加速运动,最终匀速.当R上电压达到恒定时,棒已做匀速运动.由a=0得:
mgsinθ=B3IL1
又根据闭合欧姆定律得:I=
| B3L1vm |
| R+r |
所以有:vm=
| mg(R+r)sinθ | ||||
|
| 0.2×10×(1.5+0.5)×0.5 |
| 1.52×12 |
| 8 |
| 9 |
该过程中,根据能量守恒定律得:Q总=mgxsinθ-
| 1 |
| 2 |
而 Q总=QR+Qr
| QR |
| Qr |
| R |
| r |
故 QR=
| R |
| R+r |
代入数据得:QR=1.5J
答:(1)当t=2s时,外力F1的大小是0;
(2)当t=3s前的瞬间,外力F2的大小是0.5N,方向沿斜面向下;
(3)画出前4s外力F随时间变化的图象如图所示.
(4)棒下滑该距离过程中电阻R上产生的焦耳热是1.5J.
点评:解决本题的关键掌握法拉第电磁感应定律、平衡条件、安培力公式和能量守恒定律等等电磁学和力学规律,得到解析式,再画图象是常用的思路,要多做相关的训练.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 求:
求: 如图甲所示,两根足够长的平行光滑金属导轨固定放置在水平面上,间距L=0.2m,一端通过导线与阻值为R=1Ω的电阻连接;导轨上放一质量为m=0.5kg的金属杆,金属杆与导轨的电阻均忽略不计.整个装置处于竖直向上的大小为B=0.5T的匀强磁场中.现用与导轨平行的拉力F作用在金属杆上,金属杆运动的v-t图象如图乙所示.(取重力加速度g=10m/s2)求:
如图甲所示,两根足够长的平行光滑金属导轨固定放置在水平面上,间距L=0.2m,一端通过导线与阻值为R=1Ω的电阻连接;导轨上放一质量为m=0.5kg的金属杆,金属杆与导轨的电阻均忽略不计.整个装置处于竖直向上的大小为B=0.5T的匀强磁场中.现用与导轨平行的拉力F作用在金属杆上,金属杆运动的v-t图象如图乙所示.(取重力加速度g=10m/s2)求: 如图甲所示,两根足够长的平行导轨处在与水平方向成θ角的斜面上,θ=370,导轨电阻不计,间距L=0.3m.在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场.导轨底端接一个阻值R=1Ω的电阻.质量m=1kg、电阻r=2Ω的金属棒ab横跨在平行导轨间,棒与导轨间的动摩擦因数μ=0.5,金属棒从距底端高为h1=2.0m处以平行于导轨向上的初速度v0=10m/s上滑,滑至最高点时高度为h2=3.2m,sin37°=0.6,cos37°=0.8,取g=10m/s2.
如图甲所示,两根足够长的平行导轨处在与水平方向成θ角的斜面上,θ=370,导轨电阻不计,间距L=0.3m.在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场.导轨底端接一个阻值R=1Ω的电阻.质量m=1kg、电阻r=2Ω的金属棒ab横跨在平行导轨间,棒与导轨间的动摩擦因数μ=0.5,金属棒从距底端高为h1=2.0m处以平行于导轨向上的初速度v0=10m/s上滑,滑至最高点时高度为h2=3.2m,sin37°=0.6,cos37°=0.8,取g=10m/s2.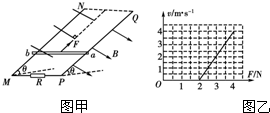 如图甲所示,两根足够长的光滑直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下.导轨和金属杆的电阻可忽略.用与导轨平行且向上的恒定拉力F作用在金属杆上,金属杆ab沿导轨向上运动,最终将做匀速运动.当改变拉力F的大小时,相对应的匀速运动速度v也会改变,v和F的关系如图乙所示.
如图甲所示,两根足够长的光滑直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下.导轨和金属杆的电阻可忽略.用与导轨平行且向上的恒定拉力F作用在金属杆上,金属杆ab沿导轨向上运动,最终将做匀速运动.当改变拉力F的大小时,相对应的匀速运动速度v也会改变,v和F的关系如图乙所示.