题目内容
消防队员为缩短下楼的时间,往往抱着竖直的杆直接滑下.假设一名质量为60kg、训练有素的消防队员从七楼(即离地面18m的高度)抱着竖直的杆以最短的时间滑下.已知杆的质量为200kg,消防队员着地的速度不能大于6m/s,手和腿对杆的最大压力为1 800N,手和腿与杆之间的动摩擦因数为0.5,设当地的重力加速度g=10m/s2.假设杆是固定在地面上的,杆在水平方向不移动.试求:
(1)消防队员下滑过程中的最大速度;
(2)消防队员下滑过程中杆对地面的最大压力;
(3)消防队员下滑的最短的时间.
解:(1)消防队员开始阶段自由下落的末速度即为下滑过程的最大速度vm,
有2gh1=vm2.
消防队员受到的滑动摩擦力
Ff=μFN=0.5×1 800 N=900 N.
减速阶段的加速度大小:
a2=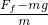 =5 m/s2
=5 m/s2
减速过程的位移为h2,由vm2-v′2=2a2h2 v′=6m/s
又h=h1+h2
以上各式联立可得:vm=12 m/s.
答:消防队员下滑过程中的最大速度为12m/s.
(2)以杆为研究对象得:
FN=Mg+Ff=2 900 N.
根据牛顿第三定律得,杆对地面的最大压力为2 900 N.
答:杆对地面的最大压力为2 900 N.
(3)最短时间为
tmin= +
+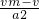 =2.4 s.
=2.4 s.
答:消防队员下滑的最短的时间为2.4s.
分析:(1)消防队员自由下落的末速度最大,根据自由下落的位移和匀减速直线运动的位移为18m,以及着地速度不超过6m/s,运用运动学公式求出下落的最大速度.
(2)当手和腿对杆有最大压力,就有最大滑动摩擦力,人所受滑动摩擦力方向向上,则杆子受滑动摩擦力向下,对杆子受力分析,求出地面对杆子的支持力,从而得出消防队员下滑过程中杆对地面的最大压力.
(3)先做自由落体运动,然后以最大加速度做匀减速直线运动,时间最短,根据速度时间公式分别求出自由落体运动时间和匀减速直线运动的时间,从而得出最短时间.
点评:解决本题的关键搞清消防员的运动过程,知道加速度是处理动力学问题的桥梁.
有2gh1=vm2.
消防队员受到的滑动摩擦力
Ff=μFN=0.5×1 800 N=900 N.
减速阶段的加速度大小:
a2=
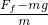 =5 m/s2
=5 m/s2减速过程的位移为h2,由vm2-v′2=2a2h2 v′=6m/s
又h=h1+h2
以上各式联立可得:vm=12 m/s.
答:消防队员下滑过程中的最大速度为12m/s.
(2)以杆为研究对象得:
FN=Mg+Ff=2 900 N.
根据牛顿第三定律得,杆对地面的最大压力为2 900 N.
答:杆对地面的最大压力为2 900 N.
(3)最短时间为
tmin=
 +
+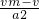 =2.4 s.
=2.4 s.答:消防队员下滑的最短的时间为2.4s.
分析:(1)消防队员自由下落的末速度最大,根据自由下落的位移和匀减速直线运动的位移为18m,以及着地速度不超过6m/s,运用运动学公式求出下落的最大速度.
(2)当手和腿对杆有最大压力,就有最大滑动摩擦力,人所受滑动摩擦力方向向上,则杆子受滑动摩擦力向下,对杆子受力分析,求出地面对杆子的支持力,从而得出消防队员下滑过程中杆对地面的最大压力.
(3)先做自由落体运动,然后以最大加速度做匀减速直线运动,时间最短,根据速度时间公式分别求出自由落体运动时间和匀减速直线运动的时间,从而得出最短时间.
点评:解决本题的关键搞清消防员的运动过程,知道加速度是处理动力学问题的桥梁.

练习册系列答案
相关题目