题目内容
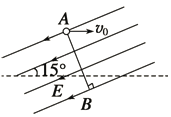
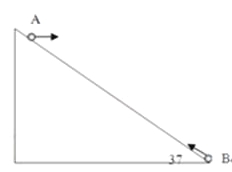
【题目】如图所示，一足够长倾角为37°的斜面固定在水平地面上，质量为m的小球B从斜面的底端开始以初速度10m/s沿斜面向上运动，与此同时质量为m的小球A在斜面上某点以水平初速度抛出，不计空气阻力。已知小球A落到斜面时恰好与小球B相撞（不考虑二次相撞），此时小球B速率为4m/s，小球B与斜面间的动摩擦因数μ＝0．5，g取10m/s2。求：小球A的初速度以及抛出点距地面的高度。（sin37°=0．6，cos37°=0．8）
【答案】（1）4．32m；（2）45．6m
【解析】试题分析：（1）若在B上滑时相撞，小球B沿斜面做匀减速直线运动，根据牛顿第二定律得：
mgsin37°+μmgcos37°=ma1
解得：a1＝10m/s2，
速率减为v1=4m/s时，有：
，
，
小球A做平抛运动，竖直方向：y1＝
gt12，
水平方向：x1=v01t1，
，
而V01=4m/s
则H1=y1+s1sin37°=4．32m
（2）若在B下滑时相撞，小球B速度减为0反向加速，根据牛顿第二定律得：mgsin37°-μmgcos37°=ma2，
代入数据解得：a2＝2m/s2；
，
，t2=t上+t下=3s，
小球A做平抛运动竖直方向：y2＝gt22
水平方向：x2=v02t2
而V02=20m/s
则H2=y2+s2sin37°=45．6m
练习册系列答案
阅读快车系列答案
相关题目
