题目内容
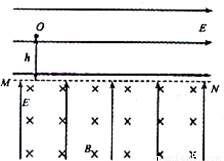
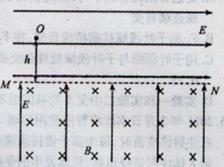
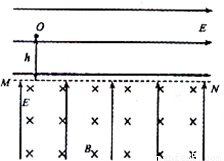
如图所示,在水平线MN上方有水平向右的匀强电场,下方有垂直纸面向里的匀强磁场和竖直向上的匀强电场.现将一质量为m、带电量为+q(q>0)的小球在MN上方高为h处由静止释放,已知两区域内的电场强度E的大小均等于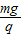 ,g为重力加速度.
,g为重力加速度.(1)求小球第一次到达MN时的速度大小和方向.
(2)小球释放后,前三次通过MN上的点依次为a,b,c(图中未标出),且线段ab=bc,求磁场的磁感应强度大小.
【答案】分析:(1)对小球进行受力分析,小球受到重力,和水平方向的电场力,小球在MN上方做匀加速直线运动,根据牛顿第二定律求出加速度,根据运动学速度-位移公式即可求解速度;
(2)在MN下方,由于mg=Eq,故小球在竖直平面内做匀速圆周运动,且圆心角为90°,根据洛伦兹力提供向心力公式求得半径,在MN上方的bc过程,小球做类平抛运动,根据平抛运动的特点联立方程即可求解.
解答:解:(1)对小球进行受力分析,小球受到重力,和水平方向的电场力,小球在MN上方做匀加速直线运动,
因为Eq=mg,所以速度方向斜向右下方45°,
根据牛顿第二定律得:
a=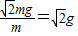
根据匀加速直线运动,速度位移公式得:
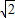 h=
h=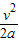
解得:v=2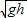
(2)在MN下方,由于mg=Eq,故小球在竖直平面内做匀速圆周运动,且圆心角为90°,
根据Bqv=m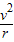
解得:r=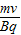
由题意得:bc=ab=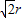 =
=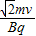
在MN上方的bc过程,小球做类平抛运动,a=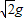
bc?cos45°=vt
bc?sin45°=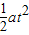
解得:B=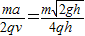
答:(1)小球第一次到达MN时的速度大小为2 ,方向斜向右下方45°;
,方向斜向右下方45°;
(2)磁场的磁感应强度大小为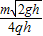 .
.
点评:本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确对粒子进行受力分析,判断粒子的运动情况,根据牛顿第二定律、运动学基本公式结合几何关系求解,难度适中.
(2)在MN下方,由于mg=Eq,故小球在竖直平面内做匀速圆周运动,且圆心角为90°,根据洛伦兹力提供向心力公式求得半径,在MN上方的bc过程,小球做类平抛运动,根据平抛运动的特点联立方程即可求解.
解答:解:(1)对小球进行受力分析,小球受到重力,和水平方向的电场力,小球在MN上方做匀加速直线运动,
因为Eq=mg,所以速度方向斜向右下方45°,
根据牛顿第二定律得:
a=
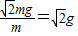
根据匀加速直线运动,速度位移公式得:
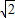 h=
h=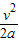
解得:v=2
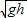
(2)在MN下方,由于mg=Eq,故小球在竖直平面内做匀速圆周运动,且圆心角为90°,
根据Bqv=m
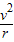
解得:r=
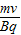
由题意得:bc=ab=
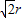 =
=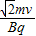
在MN上方的bc过程,小球做类平抛运动,a=
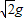
bc?cos45°=vt
bc?sin45°=
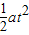
解得:B=
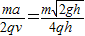
答:(1)小球第一次到达MN时的速度大小为2
 ,方向斜向右下方45°;
,方向斜向右下方45°;(2)磁场的磁感应强度大小为
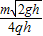 .
.点评:本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确对粒子进行受力分析,判断粒子的运动情况,根据牛顿第二定律、运动学基本公式结合几何关系求解,难度适中.

练习册系列答案
相关题目
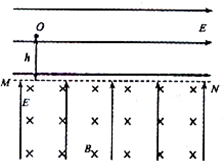 如图所示,在水平线MN上方有水平向右的匀强电场,下方有垂直纸面向里的匀强磁场和竖直向上的匀强电场.现将一质量为m、带电量为+q(q>0)的小球在MN上方高为h处由静止释放,已知两区域内的电场强度E的大小均等于
如图所示,在水平线MN上方有水平向右的匀强电场,下方有垂直纸面向里的匀强磁场和竖直向上的匀强电场.现将一质量为m、带电量为+q(q>0)的小球在MN上方高为h处由静止释放,已知两区域内的电场强度E的大小均等于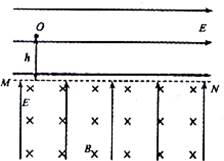
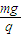 ,g为重力加速度.
,g为重力加速度.