题目内容
（16分）如图所示，在倾角θ=37°的斜面两端，垂直于斜面方向固定两个弹性板，两板相距L=2m，质量为m=10g，电荷量为q=1×10－7C的物体与斜面间的动摩擦因数为
=0.2，物体从斜面中点以大小为10m/s的速度沿斜面开始运动。若物体与弹性板碰撞过程中机械能不损失，电荷量也不变，平行于斜面向上的匀强电场的场强E=2×106N/C，（sin37°=0.6，cos37°=0.8，g取10m/s2）．求：
（1）物体在运动过程中受到斜面摩擦力f的大小；
（2）补充完整物体从斜面中点出发第一次到达上端弹性板过程的动能定理表达式，物体的初速度为v，末速度为
（全部用字母表示）；
+_______________=____________-____________
（3）物体在斜面上运动的总路程．
=0.2，物体从斜面中点以大小为10m/s的速度沿斜面开始运动。若物体与弹性板碰撞过程中机械能不损失，电荷量也不变，平行于斜面向上的匀强电场的场强E=2×106N/C，（sin37°=0.6，cos37°=0.8，g取10m/s2）．求：（1）物体在运动过程中受到斜面摩擦力f的大小；
（2）补充完整物体从斜面中点出发第一次到达上端弹性板过程的动能定理表达式，物体的初速度为v，末速度为
（全部用字母表示）；+_______________=____________-____________（3）物体在斜面上运动的总路程．
（16分）解：（1）
（5分）
（2）
（5分）
（3）S="40m " （6分）
（5分）（2）
（5分）（3）S="40m " （6分）
（16分）解：（1） （5分）
（2） （5分）
（3）mgsin37°="0.06N " Eq="0.2N " f+ mgsin37°<Eq
故最后应停在紧靠上边弹性板处，根据动能定理
解得：S="40m " （6分）
（5分）（2）
（5分）（3）mgsin37°="0.06N " Eq="0.2N " f+ mgsin37°<Eq
故最后应停在紧靠上边弹性板处，根据动能定理
解得：S="40m " （6分）
练习册系列答案
相关题目
。当传送带沿逆时针方向以v1=3m/s的速度匀速运动时，将小物块无初速地放在A点后，它会运动至B点。（g取10m/s2））
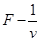图象（图中AB、BO均为直线）。假设电动车行驶中所受的阻力恒定，下面关于电动车的检测数据说法正确的（ ）
如图，光滑水平面AB与竖直面的半圆形导轨在B点相连接，导轨半径为R，一质量为m的静止木块在A处压缩弹簧，释放后，木块获得一向右的初速度，当它经过B点进入导轨瞬间对导轨的压力是其重力的7倍，之后向上运动恰能通过轨道顶点C，不计空气阻力，试求：