题目内容
（2010?武汉二模）一滑雪运动员以滑雪板和滑雪杖为工具在平直雪道上进行滑雪训练．某次训练中，他站在雪道上第一次利用滑雪杖对雪面的作用获得水平推力F=60N而向前滑行，其作用时间为t1=1s，撤除水平推力F后经过t2=2s，他第二次利用滑雪杖对雪面的作用获得同样的水平推力且其作用时间仍为1s．已知该运动员连同装备的总质量为m=50kg，在整个运动过程中受到的滑动摩擦力大小恒为f=10N，求该运动员（可视为质点）第二次撤除水平推力后滑行的最大距离．
分析：由题，分析可知：滑雪运动员利用滑雪杖对雪面的作用获得水平推力F时做匀加速直线运动，撤除水平推力F后做匀减速直线运动，根据牛顿第二定律和速度公式求出第二次刚撤除水平推力F时的速度．再由速度位移关系式求解第二次撤除水平推力后滑行的最大距离．
解答：解：运动员站在雪道上第一次利用滑雪杖对雪面作用时，
加速度为 a1=
=1m/s2
t1=1s时的速度为 v1=a1t1=1m/s
第一次撤除水平推力F后，加速度为
a2=-
=-0.2m/s2
撤除水平推力F后经过t2=2s，速度为
v1′=v1+a2t2=0.6m/s
第二次刚撤除水平推力F时，速度为
v2=v1′+a1t1=1.6m/s
此后在水平方向仅受摩擦力作用做匀减速运动，滑行的最大距离为
s=
解得 s=6.4m
答：该运动员第二次撤除水平推力后滑行的最大距离为6.4m．
加速度为 a1=
| F-f |
| m |
t1=1s时的速度为 v1=a1t1=1m/s
第一次撤除水平推力F后，加速度为
a2=-
| f |
| m |
撤除水平推力F后经过t2=2s，速度为
v1′=v1+a2t2=0.6m/s
第二次刚撤除水平推力F时，速度为
v2=v1′+a1t1=1.6m/s
此后在水平方向仅受摩擦力作用做匀减速运动，滑行的最大距离为
s=
0-
| ||
| 2a2 |
解得 s=6.4m
答：该运动员第二次撤除水平推力后滑行的最大距离为6.4m．
点评：本题过程较多，要边计算边分析，也可以通过作速度-时间图象分析运动过程．
练习册系列答案
相关题目
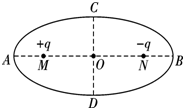（2010?武汉二模）如图所示，虚线AB和CD分别为椭圆的长轴和短轴，相交于O点，两个等量异种点电荷分别处于椭圆的两个焦点M、N上，下列说法中正确的是（ ）
（2010?武汉二模）如图所示，在空间有一坐标系xoy，直线OP与x轴正方向的夹角为30°，第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II，直线OP是他们的边界，OP上方区域I中磁场的磁感应强度为B．一质量为m，电荷量为q的质子（不计重力）以速度v从O点沿与OP成30°角的方向垂直磁场进入区域I，质子先后通过磁场区域I和II后，恰好垂直打在x轴上的Q点（图中未画出），试求：