题目内容
16. 如图所示,长为l的绝缘细线一端悬于O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O?点.现将此装置放在水平向右的匀强电场中,小球能够静止在A点.此时细线与竖直方向成θ角.若已知当地的重力加速度大小为g,求:
如图所示,长为l的绝缘细线一端悬于O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O?点.现将此装置放在水平向右的匀强电场中,小球能够静止在A点.此时细线与竖直方向成θ角.若已知当地的重力加速度大小为g,求:(1)该匀强电场的电场强度大小为多少?
(2)若将小球从O′点由静止释放,则小球运动到A点时的速度有多大?
(3)若将小球从O′点由静止释放,则小球运动到A点时绝缘细线的拉力?
分析 (1)由题细线向右偏离竖直方向,小球受到的电场力水平向右,根据电场力方向与电场强度方向的关系和根据平衡条件求出电量.
(2)若将小球从O′点由静止释放,则小球运动到A点的过程中,电场力做正功,重力做负功,总功等于小球动能的变化.
(3)在A点,拉力、重力、电场力的合力提供向心力,根据牛顿第二定律列式求解.
解答 解:(1)小球在A点受到竖直向下的重力、拉力和水平向右的电场力,根据共点力平衡条件,有:
$\frac{qE}{mg}$=tanθ
解得:
E=$\frac{mgtanθ}{q}$
(2)小球运动到A点的过程中,电场力做正功,重力做负功,根据动能定理,有:
E•q$\frac{l}{sinθ}$-mgl(1-cosθ)=$\frac{1}{2}$mv2
解得:
v=$\sqrt{\frac{2gl(1-cosθ)}{cosθ}}$
(3)在A点,合力提供向心力,故:
T-$\frac{mg}{cosθ}$=m$\frac{{v}^{2}}{l}$
解得:
T=($\frac{3}{cosθ}$-2)mg
答:(1)该匀强电场的电场强度大小为$\frac{mgtanθ}{q}$;
(2)若将小球从O′点由静止释放,则小球运动到A点时的速度为$\sqrt{\frac{2gl(1-cosθ)}{cosθ}}$;
(3)若将小球从O′点由静止释放,则小球运动到A点时绝缘细线的拉力为=($\frac{3}{cosθ}$-2)mg.
点评 本题是平衡条件、牛顿第二定律和动能定理的综合应用.此题中小球的运动可运用单摆运动类比.

练习册系列答案
相关题目
4.一质点做直线运动,当时间t=t0时,位移s>0,速度v>0,加速度a>0,此后a逐渐减少直到a=0,则它的( )
| A. | 速度逐渐减小 | B. | 位移始终为正值,速度变为负值 | ||
| C. | 速度变化越来越慢 | D. | 位移的变化越来越慢 |
1.一物体由静止开始做匀加速直线运动,在t s内通过位移x m,则它从出发开始通过$\frac{x}{4}$m所用的时间为( )
| A. | $\frac{t}{4}$ | B. | $\frac{t}{2}$ | C. | $\frac{t}{16}$ | D. | $\frac{t}{22}$ |
5.如图,对两个电量均为+q的点电荷连线中点O和中垂线上某点P,正确的关系是( )


| A. | U0<Up,E0>Ep | |
| B. | U0>UP,E0>Ep | |
| C. | 将正电荷从O点移到P点,电场力做正功 | |
| D. | 将正电荷从O点移到P点,电场力做负功 |
 如图所示,A、B两木块的质量mA=0.5kg,mB=0.2kg.A放在水平桌面上且与桌面的最大静摩擦力为1N,欲使A保持静止,则拉力F应在什么范围内?(g取10n/kg)
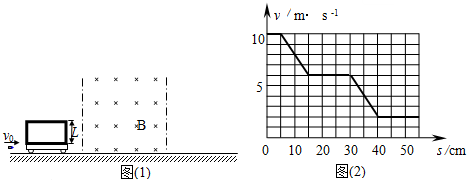
如图所示,A、B两木块的质量mA=0.5kg,mB=0.2kg.A放在水平桌面上且与桌面的最大静摩擦力为1N,欲使A保持静止,则拉力F应在什么范围内?(g取10n/kg) 高一年级某“机器人”社团对自制的一辆电动遥控小车的性能进行研究,他们让小车在水平直轨道上由静止开始始终以额定功率运动,经过t=5s时小车达到最大速度,小车在运动的过程中的部分v-t图象如图所示,已知小车质量m=1kg,在运动过程中受到阻力大小恒为车重的0.1倍,g取10m/s2,求:
高一年级某“机器人”社团对自制的一辆电动遥控小车的性能进行研究,他们让小车在水平直轨道上由静止开始始终以额定功率运动,经过t=5s时小车达到最大速度,小车在运动的过程中的部分v-t图象如图所示,已知小车质量m=1kg,在运动过程中受到阻力大小恒为车重的0.1倍,g取10m/s2,求: