题目内容
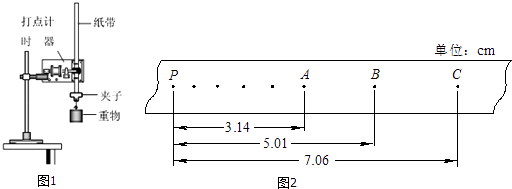
【题目】小球沿斜面做匀加速直线运动．在A位置开始计时，连续相等时间t内记录到小球位置如图，d1、d2、d3分别为位置B、C、D到A的距离．则（ ）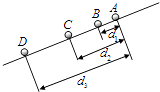
A.（d3﹣d2）=（d2﹣d1）
B.小球在B时的速度为 
C.小球在C时的速度为 
D.小球运动的加速度为 
【答案】C
【解析】解：A、（d3﹣d2）是第3个t内的位移，而（d2﹣d1）是第2个t时间内的位移，因为小球做匀加速运动，故位移不等，A错误；
B、小球在B点的瞬时速度等于AC的平均速度故 
，故B错误；
C、小球在C点的瞬时速度等于BD的平均速度即 
，故C正确；
D、根据△x=aT2可得加速度 
，d3﹣d2是小球第3个t时间内的位移，故D错误．
故选：C．
运用匀变速直线运动规律推论求解，中间时刻的瞬时速度等于全程的平均速度，及△x=aT2求解瞬时速度和加速度．
练习册系列答案
相关题目
【题目】一列火车和一辆汽车沿同一方向做匀变速直线运动，速度分别为v1和v2 ． t=0时刻，火车在汽车前方26m处，此后v1、v2在各个时刻的大小如表所示．根据表格中的数据，通过计算求：
t/s | 0 | 1 | 2 | 3 | 4 | 5 |
v1/ms﹣1 | 16.0 | 14.0 | 12.0 | 10.0 | … | … |
v2/ms﹣1 | 4.0 | 5.0 | 6.0 | 7.0 | … | … |
（1）两车经过多长时间相距最大？此时最大间距是多少？
（2）经过多长时间两车相遇？
（3）两车初始间距满足什么条件可以相遇两次．
