题目内容
【题目】某同学通过Internet查询到“神舟”六号飞船在圆形轨道上运行一周的时间约为90分钟，他将这一信息与地球同步卫星进行比较，由此可知（ ）
A. “神舟”六号在圆形轨道上运行时的向心加速度比地球同步卫星大
B. “神舟”六号在圆形轨道上运行时的速率比地球同步卫星大
C. “神舟”六号在圆形轨道上运行时离地面的高度比地球同步卫星高
D. “神舟”六号在圆形轨道上运行时的角速度比地球同步卫星小
【答案】AB
【解析】试题分析：C．根据
=m
得：
T=2π
，“神舟”六号飞船的周期比同步卫星短，所以，“神舟”六号飞船的半径比同步卫星小，
所以“神舟”六号在圆形轨道上运行时离地面的高度比地球同步卫星低，故C错误；
A．根据
=ma，得：a=
，“神舟”六号飞船的半径比同步卫星小，所以，“神舟”六号飞船的向心加速度比同步卫星大，故A正确；
B．根据=m
，
解得v=
，“神舟”六号飞船的半径比同步卫星小，所以，“神舟”六号飞船的线速度比同步卫星大，故B正确；
D．根据ω=
知，“神舟”六号飞船的周期比同步卫星短，所以，“神舟”六号飞船的角速度比同步卫星大，故D错误．
故选：AB．
阅读快车系列答案
【题目】如图甲所示，用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系。
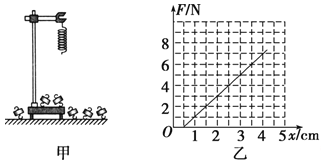
（1）为完成实验，还需要的实验器材有______________。
（2）实验中需要测量的物理量有______________。
（3）图乙是弹簧弹力F与弹簧伸长量x的F－x图线，由此可求出弹簧的劲度系数为____________ N/m。图线不过原点的原因是由于_______________。
（4）为完成该实验，设计的实验步骤如下：
A．以弹簧伸长量为横坐标，以弹力为纵坐标，描出各组（x，F）对应的点，并用平滑的曲线连接起来； |
B．记下弹簧不挂钩码时其下端的刻度尺上的刻度l0； |
C．将铁架台固定于桌子上，并将弹簧的一端系于横梁上，在弹簧附近竖直固定一把刻度尺； |
D．依次在弹簧下端挂上1个、2个、3个、4个…钩码，并分别记下钩码静止时弹簧下端所对应的刻度，并记录在表格内，然后取下钩码； |
E．以弹簧伸长量为自变量，写出弹力与伸长量的关系式。首先尝试写成一次函数，如果不行，则考虑二次函数；
F．解释函数表达式中常数的物理意义；
G．整理仪器。
请将以上步骤按操作的先后顺序排列出来：________。
