题目内容
19. 如图所示是一个特殊形状的气缸的截面图,它由上、下两部分圆柱形气缸连接而成,上、下两部分气缸内部的横截面积分别为S1=20cm2和S2=10cm2,两只活塞的质量分别为m1=1.6kg和m2=0.4kg,用一根长L=30cm的轻绳相连.活塞封闭性良好,跟气缸壁的摩擦不计.初状态时大气压为p0=1.0×105Pa,温度为227℃,两活塞静止,缸内封闭气体的体积为500mL.求:
如图所示是一个特殊形状的气缸的截面图,它由上、下两部分圆柱形气缸连接而成,上、下两部分气缸内部的横截面积分别为S1=20cm2和S2=10cm2,两只活塞的质量分别为m1=1.6kg和m2=0.4kg,用一根长L=30cm的轻绳相连.活塞封闭性良好,跟气缸壁的摩擦不计.初状态时大气压为p0=1.0×105Pa,温度为227℃,两活塞静止,缸内封闭气体的体积为500mL.求:(1)当温度降低到多少时,上面的活塞恰好下降到粗细两部分气缸的交界处?
(2)当温度降低到多少时,连接两个活塞的轻绳中的张力刚好等于零?
(3)为了使下面这只活塞回到初状态时的位置,需要把温度继续降低到多少?(取g=10m/s2)
分析 (1)以两只活塞和细绳组成的整体研究对象,根据平衡条件求出初态时封闭气体的压强.
上面的活塞下降到粗细两部分气缸的交界处的过程中,封闭气体发生等压变化,根据吕萨克定律求解温度;
(2)由平衡条件求出绳子拉力为零时气体的压强,此过程气体发生等容变化,应用查理定律可以求出气体的温度;
(3)气体发生等压变化,应用盖吕萨克定律可以求出气体的温度.
解答 解:(1)设初态时封闭气体的压强为P1,以两只活塞和细绳组成的整体研究对象,根据平衡条件得:
P1(S1-S2)=(m1+m2)g+P0(S1-S2),
解得:P1=P0+$\frac{({m}_{1}+{m}_{2})g}{{S}_{1}-{S}_{2}}$=1.2×105Pa
上面的活塞下降到粗细两部分气缸的交界处的过程中,封闭气体的压强不变,发生等压变化.
由盖吕萨克定律得:$\frac{{V}_{1}}{{T}_{1}}$=$\frac{{V}_{2}}{{T}_{2}}$,其中:V1=5.0×10-4m3,T1=227+273=500K,V2=S2L=3.0×10-4m3,
解得:T2=300K;
(2)绳子拉力恰好为0时,气体的压强:p3=p0-$\frac{{m}_{2}g}{{S}_{2}}$=0.96×105Pa,T2=300K,p2=1.2×105Pa,T3=?
气体发生等容变化,由查理定律得:$\frac{{p}_{2}}{{T}_{2}}$=$\frac{{p}_{3}}{{T}_{3}}$,
代入数据解得:T3=240K;
(3)设下面活塞下降的距离为h,则有:V1-V2=(S1-S2)h,
代入数据解得:h=0.2m,
下面的活塞回到初始位置时气体体积为:V4=V2-S2h=1×10-4m3,
在此过程中,气体发生等压变化,由盖吕萨克定律得:$\frac{{V}_{3}}{{T}_{3}}$=$\frac{{V}_{4}}{{T}_{4}}$,
代入数据解得:T4=80K;
答:(1)当温度降低到300K时,上面的活塞恰好下降到粗细两部分气缸的交界处;
(2)当温度降低到240K时,连接两个活塞的轻绳中的张力刚好等于零;
(3)为了使下面这只活塞回到初状态时的位置,需要把温度继续降低到80K.
点评 本题考查了求气体的温度,分析清楚气体状态变化过程是解题的关键,应用平衡条件求出气体的压强,应用盖吕萨克定律与查理定律可以解题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 如图所示,在粗糙水平面上有一个较大的三角形物块,小物块P正沿它的光滑左侧面加速下滑,而小物块Q在它的粗糙右侧面上和大物块都静止,以下判断正确的是( )
如图所示,在粗糙水平面上有一个较大的三角形物块,小物块P正沿它的光滑左侧面加速下滑,而小物块Q在它的粗糙右侧面上和大物块都静止,以下判断正确的是( )| A. | P、Q都受三个力作用:沿斜面方向P受的是下滑力,而Q受的是摩擦力 | |
| B. | 地面受大物块的压力小于三者重力之和 | |
| C. | 地面给大物块的静摩擦力水平向左,使大物块有向左运动的趋势 | |
| D. | 如果左侧面也粗糙,且使得P匀速下滑,则静止的大物块不受地面摩擦力作用 |
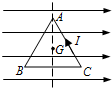 如图所示,有一正三角形线圈ABC,通过逆时针方向的电流,现有一水平匀强磁场沿BC方向向右,则线圈运动情况是( )
如图所示,有一正三角形线圈ABC,通过逆时针方向的电流,现有一水平匀强磁场沿BC方向向右,则线圈运动情况是( )| A. | 以底边BC为轴转动,A向纸面外 | B. | 以中心G为轴,在纸面逆时针转动 | ||
| C. | 以中线AM为轴,逆时针转动(俯视) | D. | 受合力为零,故不转动 |
| A. | 45MHz | B. | 50MHz | C. | 20MHz | D. | 6MHz |
| A. | 计价器上显示的公里数6.2表示位移 | |
| B. | 80km/h表示的是瞬时速率 | |
| C. | 全程的平均速率约为30km/h | |
| D. | 10时42分是时间 |
 如图所示,线圈ab、bc的边长分别为L1、L2,通以电流I,开始时线圈平面与匀强磁场B的磁感线平行,当线圈绕OO′轴转过θ角时( )
如图所示,线圈ab、bc的边长分别为L1、L2,通以电流I,开始时线圈平面与匀强磁场B的磁感线平行,当线圈绕OO′轴转过θ角时( )| A. | 线圈的ab边所受安培力的大小为BIL1cosθ | |
| B. | 线圈的ab边所受安培力的大小为BIL1 | |
| C. | 线圈所受的磁力矩为BIL1L2cosθ | |
| D. | 线圈所受的磁力矩为BIL1L2 |
 如图所示,轻绳CD上端固定在天花板上,下端系一个轻质光滑的滑轮.轻绳AB的A端固定在天花板上,B端跨过滑轮后系一个重50N的物体.稳定后轻绳AB的上段与水平面的夹角是30°.试求:
如图所示,轻绳CD上端固定在天花板上,下端系一个轻质光滑的滑轮.轻绳AB的A端固定在天花板上,B端跨过滑轮后系一个重50N的物体.稳定后轻绳AB的上段与水平面的夹角是30°.试求:
 在“练习使用多用电表”实验时:
在“练习使用多用电表”实验时: