题目内容
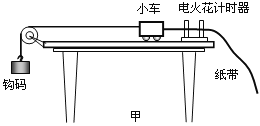
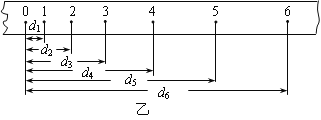
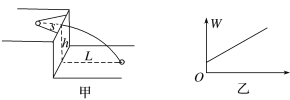
【题目】在“探究功与速度变化的关系”实验中，采用如图甲所示装置，水平正方形桌面距离地面高度为h，将橡皮筋的两端固定在桌子边缘上的两点，将小球置于橡皮筋的中点，向左移动距离s，使橡皮筋产生形变，由静止释放后，小球飞离桌面，测得其平抛的水平射程为L.改变橡皮筋的条数，重复实验.
(1)实验中，小球每次释放的位置到桌子边缘的距离s应________(选填“不同”“相同”或“随意”).
(2)取橡皮筋对小球做功W为纵坐标，为了在坐标系中描点得到一条直线，如图乙所示，应选__________(填“L”或“L2”)为横坐标.若直线与纵轴的截距为b，斜率为k，可求小球与桌面间的动摩擦因数为__________(使用题中所给符号表示).
【答案】(1)相同 (2)L2 
【解析】(1)为保证每根橡皮筋的形变量相等，即每根橡皮筋弹力做的功相等，故小球每次释放的位置到桌子边缘的距离s要相同；
(2)小球抛出后做平抛运动，由h＝
gt2，
得：t＝
，初速度v＝
＝L
，
由动能定理：W－μmgs＝
mv2＝
m
L2，
得W＝
＋μmgs
故应选L2为横坐标，则有：k＝
，b＝μmgs，
得：μ＝.
练习册系列答案
相关题目
