题目内容
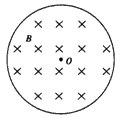
如图所示，有一个垂直纸面向里的匀强磁场，磁感应强度B=0.8 T，磁场有明显的圆形边界，圆心为O，半径为1.0 cm，现在纸面内先后放上圆线圈，圆心均在O处，A线圈半径为1.0 cm，10匝；B线圈半径为2.0 cm，1匝；C线圈半径为0.5 cm，1匝。问：
(1)在B减为0.4 T的过程中，A 和B中磁通量各改变多少？
(2)当磁场方向转过30°角的过程中，C中的磁通量改变多少？
(1)在B减为0.4 T的过程中，A 和B中磁通量各改变多少？
(2)当磁场方向转过30°角的过程中，C中的磁通量改变多少？
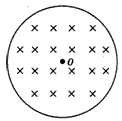
解：(1)A线圈半径为1.0 cm，正好和圆形磁场区域的半径相等，而B线圈半径为2.0 cm，大于圆形磁场区域的半径，但穿过A、B线圈的磁感线的条数相等，因此在求通过B线圈中的磁通量时，面积S只能取圆形磁场区域的面积，即A、B中的磁通量的变化量相等
设圆形磁场区域的半径为R，对线圈A，φ=BπR2
磁通量的改变量：△φA=|φ2-φ1|=(B2-B1)πR2=(0.8-0.4)×3.14×(10-2)2 Wb=1.256×10-4 Wb
同理，△φB=1.256×10-4 Wb
(2)原图中线圈平面与磁场方向垂直，若用公式φ=BSsinθ求磁通量，此时θ1=90°
当磁场方向转过30°角时，磁场方向与线圈平面之间的夹角为θ2=60°
对线圈C：设C线圈的半径为r，φ1'=Bπr2sinθ1，φ2'=Bπr2sinθ2
磁通量的改变量：△φ=|φ2'-φ1'|=Bπr2(sin90°-sin60°)=0.8×3.14×(5×10-3)2×(1-0.866) Wb=8.4×10-6 Wb
设圆形磁场区域的半径为R，对线圈A，φ=BπR2
磁通量的改变量：△φA=|φ2-φ1|=(B2-B1)πR2=(0.8-0.4)×3.14×(10-2)2 Wb=1.256×10-4 Wb
同理，△φB=1.256×10-4 Wb
(2)原图中线圈平面与磁场方向垂直，若用公式φ=BSsinθ求磁通量，此时θ1=90°
当磁场方向转过30°角时，磁场方向与线圈平面之间的夹角为θ2=60°
对线圈C：设C线圈的半径为r，φ1'=Bπr2sinθ1，φ2'=Bπr2sinθ2
磁通量的改变量：△φ=|φ2'-φ1'|=Bπr2(sin90°-sin60°)=0.8×3.14×(5×10-3)2×(1-0.866) Wb=8.4×10-6 Wb
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013?开封一模）如图所示，有一个等腰直角三角形的匀强磁场区域，其直角边长为L，磁场方向垂直纸面向外，磁感应强度大小为B．一边长为L总电阻为R的正方形导线框abcd，从图示位置开始沿x轴正方向以速度v匀速穿过磁 场区域．取沿a→b→c→d→a的感应电流为正，则表示线框中电流i随bC边的位置坐标x变化的图象正确的是（ ）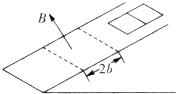
如图所示，有一个倾角为θ的足够长的斜面，沿着斜面有一宽度为2b的匀强磁场，磁感应强度为B，方向垂直斜面向外，磁场的边界与底边平行．现有一质量为m的“日”字形导线框，框上两个小正方形的边长均为b．其中三条平行边和斜面底边及磁场边界平行，电阻均为R，其余两条长平行边不计电阻．现将导线框由静止开始释放，整个框和斜面的动摩擦因数为μ（μ＜tanθ），当它刚滑进磁场时恰好做匀速直线运动．问：
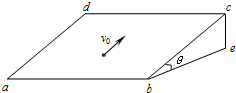如图所示，有一个足够大的倾角为θ的光滑绝缘斜面体．在空间加上一个垂直于斜面的匀强磁场，磁感应强度为B，一个质量为m、带电量为+q的小球，以初速度v0沿斜面向上运动，经过一段时间后，发现小球的速度大小仍然为v0，但方向相反；现将匀强磁场撤去，换成一个平行于be向里的水平匀强电场，场强大小为E，若小球仍以初速度v0沿斜面向上运动，求经过同样的时间后小球的速度大小．（小球的重力与所受电场力、洛伦兹力相比较，可忽略不计）