题目内容
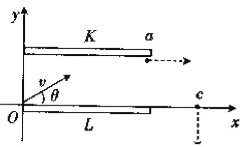
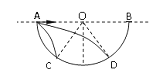
【题目】如图所示，小球A、B质量相同，分别连接在轻质细杆的两端，可绕过细杆中点O的固定水平轴自由转动．现给小球一初速度，使它们做圆周运动，当小球B运动到轨道的最低点时，细杆对小球B的作用力竖直向上，大小是小球B的重力的2倍；此时小球A运动到轨道的最高点，则细杆对小球A的作用力是（ ）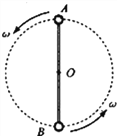
A. 方向竖直向上，大小等于小球A的重力 B. 方向竖直向下，大小等于小球A的重力 C. 方向竖直向下，大小等于小球A的重力的2倍 D. 大小等于零
【答案】D
【解析】在最低点，小球受到重力与弹力，合力提供向心力，则有： 
；
因
，所以
；
在最高点A，小球受到重力和弹力，合力提供向心力，假设弹力向下，且
则，根据牛顿第二定律，则有： 
；
综合以上公式，可解得： 
；D正确；ABC错误；
故选D。
练习册系列答案
相关题目
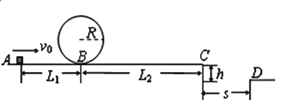
【题目】某同学利用竖直上抛小球的频闪照片验证机械能守恒定律．频闪仪每隔0.05 s闪光一次，图7中所标数据为实际距离，该同学通过计算得到不同时刻的速度如下表(当地重力加速度取9.8 m/s2，小球质量m＝0.2 kg，计算结果保留三位有效数字):
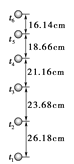
时刻 | t2 | t3 | t4 | t5 |
速度(m·s－1) | 4.99 | 4.48 | 3.98 |
(1)由频闪照片上的数据计算t5时刻小球的速度v5＝________m/s；
(2)从t2到t5时间内，重力势能增量ΔEp＝________J，动能减少量ΔEk＝________ J；
(3)在误差允许的范围内，若ΔEp与ΔEk近似相等，从而验证了机械能守恒定律．由上述计算得ΔEp________ΔEk(选填“＞”“＜”或“＝”).
