题目内容
5．
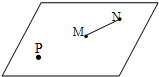如图所示，光滑绝缘的水平桌面上，固定着一个带电量为+Q的小球P，带电量分别为-q和+2q的小球M和N由绝缘细杆相连，静止在桌面上，P与M相距L，P、M和N均视为点电荷，则M与N的距离为（$\sqrt{2}$-1）L，若将M与N绕绝缘杆的中点在水平面内缓慢转动180°，外力克服电场力做功△E，则+Q的电场在绝缘杆两端的电势差UMN为$\frac{△E}{3q}$．
分析 对M、N分析，抓住MN处于平衡，根据共点力平衡，结合库仑定律求出M、N间的距离．根据电场力做功的代数和，结合电场力做功与电势差的关系求出M、N两点间的电势差．
解答 解：对M、N分别受力分析，根据库仑定律，因为M、B处于平衡，设M与N间距为r，则有：$k\frac{Qq}{{L}^{2}}=k\frac{Q•2q}{（L+r）^{2}}$，
解得r=（$\sqrt{2}$-1）L．
因为外力克服电场力做功△E，则有：-qUMN-2qUMN=-△E，
解得${U}_{MN}=\frac{△E}{3q}$．
故答案为：（$\sqrt{2}$-1）L，$\frac{△E}{3q}$
点评 本题考查了平衡以及电场力做功与电势差的关系，知道电场力做功与电势差的关系，知道△E为克服电场力做功的代数和．难度中等．
练习册系列答案
相关题目
如图所示，一小物块从倾角θ=37°的斜面上的A点由静止开始滑下，最后停在水平面上的C点．已知小物块的质量m=0.10kg，小物块与斜面和水平面间的动摩擦因数均为μ=0.25，A点到斜面底端B点的距离L=0.50m，斜面与水平面平滑连接，小物块滑过斜面与水平面连接处时无机械能损失．取sin37°=0.6，cos37°=0.8，g=10m/s2．求：
16．
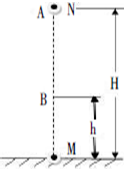在水平地面上固定一带正电小球M，另有一带电量为q（q＞0）、质量为m的小球N，从M球正上方H高处的A点以初速度v0竖直向下运动，当其运动至离地面高h处的B点时返回．若小球N始终在竖直方向运动，运动过程中不计空气阻力，两小球带电量保持不变且可视为质点，重力加速度为g，则下列说法正确的是（ ）
在水平地面上固定一带正电小球M，另有一带电量为q（q＞0）、质量为m的小球N，从M球正上方H高处的A点以初速度v0竖直向下运动，当其运动至离地面高h处的B点时返回．若小球N始终在竖直方向运动，运动过程中不计空气阻力，两小球带电量保持不变且可视为质点，重力加速度为g，则下列说法正确的是（ ）| A． | 小球N向下运动的过程中，可能一直减速，且加速度大小一直在增大 | |
| B． | 小球N向下运动的过程中，电场力做负功，系统的机械能一直增加 | |
| C． | 小球N向上运动的过程中，最高只能到达A点上方$\frac{{{v}_{0}}^{2}}{2g}$处 | |
| D． | AB两点电势差为UAB=$\frac{2mg（H-h）+m{{v}_{0}}^{2}}{2q}$ |
20．某辆汽车以相同功率在两种不同的水平路面上行驶，受到的阻力分别为车重的k1和k2倍，最大速率分别为v1和v2，则（ ）
| A． | v2=k1v1 | B． | v2=k2v1 | C． | v2=$\frac{{k}_{2}}{{k}_{1}}$v1 | D． | v2=$\frac{{k}_{1}}{{k}_{2}}$v1 |
10．某研究性学习小组用如图1所示装置来测定当地重力加速度，主要操作如下：
①由静止释放小铁球，用光电计时器记录小铁球在两个光电门间的运动时间t；
②用刻度尺测量出两个光电门之间的高度h，并计算出小铁球通过两光电门间的平均速度$\overline{v}$；
③保持光电门1的位置不变，改变光电门2的位置，重复①的操作．测出多组（h，t），计算出对应的平均速度$\overline{v}$；
④在如图2中画出$\overline{v}$-t图象．
请根据实验，回答如下问题：
（1）设小铁球到达光电门1时的速度为v0，当地的重力加速度为g．则小铁球通过两光电门间平均速度$\overline{v}$的表达式为$\overline{v}$=v0+$\frac{1}{2}$gt；（用v0、g和t表示）
（2）实验测得的数据如表：请在坐标纸上画出$\overline{v}$-t图象；
（3）根据$\overline{v}$-t图象，可以求得当地重力加速度g=9.7m/s2，试管夹到光电门1的距离约为6.2cm．
①由静止释放小铁球，用光电计时器记录小铁球在两个光电门间的运动时间t；
②用刻度尺测量出两个光电门之间的高度h，并计算出小铁球通过两光电门间的平均速度$\overline{v}$；
③保持光电门1的位置不变，改变光电门2的位置，重复①的操作．测出多组（h，t），计算出对应的平均速度$\overline{v}$；
④在如图2中画出$\overline{v}$-t图象．
请根据实验，回答如下问题：
（1）设小铁球到达光电门1时的速度为v0，当地的重力加速度为g．则小铁球通过两光电门间平均速度$\overline{v}$的表达式为$\overline{v}$=v0+$\frac{1}{2}$gt；（用v0、g和t表示）
（2）实验测得的数据如表：请在坐标纸上画出$\overline{v}$-t图象；
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| h（cm） | 10.00 | 20.00 | 30.00 | 40.00 | 50.00 | 60.00 |
| t（s） | 0.069 | 0.119 | 0.159 | 0.195 | 0.226 | 0.255 |
| $\overline{v}$（m/s） | 1.45 | 1.68 | 1.89 | 2.05 | 2.21 | 2.35 |
17．
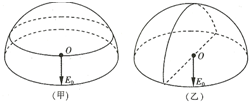一半径为R的半球面均匀带有正电荷Q，电荷Q在球心O处产生的场强大小E0=$\frac{kQ}{2{R}^{2}}$，方向如图所示．把半球面分为表面积相等的上、下两部分，如图甲所示，上、下两部分电荷在球心O处产生电场的场强大小分别为E1、E2；把半球面分为表面积相等的左、右两部分，如图乙所示，左、右两部分电荷在球心O处产生电场的场强大小分别为E3、E4．则（ ）
一半径为R的半球面均匀带有正电荷Q，电荷Q在球心O处产生的场强大小E0=$\frac{kQ}{2{R}^{2}}$，方向如图所示．把半球面分为表面积相等的上、下两部分，如图甲所示，上、下两部分电荷在球心O处产生电场的场强大小分别为E1、E2；把半球面分为表面积相等的左、右两部分，如图乙所示，左、右两部分电荷在球心O处产生电场的场强大小分别为E3、E4．则（ ）| A． | E1＜$\frac{kQ}{4{R}^{2}}$ | B． | E2=$\frac{kQ}{4{R}^{2}}$ | C． | E3＞$\frac{kQ}{4{R}^{2}}$ | D． | E4=$\frac{kQ}{4{R}^{2}}$ |
14．
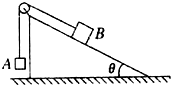如图所示，表面粗糙、倾角为θ的固定斜面顶端安装一定滑轮，小物块A、B用轻绳连接并跨过滑轮．初始时刻，A、B处于静止状态且B不受摩擦力．现施加一沿斜面向下的恒力F，使B沿斜面下滑，当质量为m的A物块上升h高度的过程中（不计滑轮的质量和摩擦）（ ）
如图所示，表面粗糙、倾角为θ的固定斜面顶端安装一定滑轮，小物块A、B用轻绳连接并跨过滑轮．初始时刻，A、B处于静止状态且B不受摩擦力．现施加一沿斜面向下的恒力F，使B沿斜面下滑，当质量为m的A物块上升h高度的过程中（不计滑轮的质量和摩擦）（ ）| A． | A、B组成的系统机械能守恒 | B． | A、B组成的系统机械能增加Fh | ||
| C． | A、B组成的系统动能增加Fh | D． | 物块B重力势能减少mgh |
15．
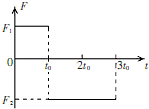一静止的物体所受到的合外力随时间的变化关系如图所示，图中F1、F2未知．已知物体从t=0时刻出发，在3t0时刻恰又返回到出发点，则（ ）
一静止的物体所受到的合外力随时间的变化关系如图所示，图中F1、F2未知．已知物体从t=0时刻出发，在3t0时刻恰又返回到出发点，则（ ）| A． | O～to物体做匀加速直线运动，to-3to物体做匀减速直线运动 | |
| B． | 物体在F1作用下的位移与在F2作用下的位移相等 | |
| C． | t0时刻物体的速度与3t0时刻物体的速度大小之比为$\frac{2}{3}$ | |
| D． | F1与F2大小之比为$\frac{6}{5}$ |