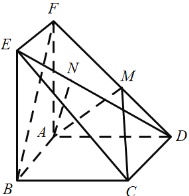
【题目】某公司为了鼓励运动提高所有用户的身体素质,特推出一款运动计步数的软件,所有用户都可以通过每天累计的步数瓜分红包,大大增加了用户走步的积极性,所以该软件深受广大用户的欢迎.该公司为了研究“日平均走步数和性别是否有关”,统计了2019年1月份所有用户的日平均步数,规定日平均步数不少于8000的为“运动达人”,步数在8000以下的为“非运动达人”,采用按性别分层抽样的方式抽取了100个用户,得到如下列联表:
运动达人 | 非运动达人 | 总计 | |
男 | 35 | 60 | |
女 | 26 | ||
总计 | 100 |
(1)(i)将![]() 列联表补充完整;
列联表补充完整;
(ii)据此列联表判断,能否有![]() 的把握认为“日平均走步数和性别是否有关”?
的把握认为“日平均走步数和性别是否有关”?
(2)将频率视作概率,从该公司的所有人“运动达人”中任意抽取3个用户,求抽取的用户中女用户人数的分布列及期望.
附:
|
|
|
|
|
|
|
|
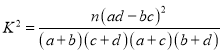
【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿,使房价快速走高,为抑制房价过快上涨,政府从2019年2月开始采用实物补偿方式(以房换房),3月份开始房价得到很好的抑制,房价渐渐回落,以下是2019年2月后该区新建住宅销售均价的数据:
月份 | 3 | 4 | 5 | 6 | 7 |
价格 | 83 | 82 | 80 | 78 | 77 |
(1)研究发现,3月至7月的各月均价![]() (百元/平方米)与月份
(百元/平方米)与月份![]() 之间具有较强的线性相关关系,求价格
之间具有较强的线性相关关系,求价格![]() (百元/平方米)关于月份
(百元/平方米)关于月份![]() 的线性回归方程;
的线性回归方程;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的销售均价的估计值,3月份至7月份销售均价估计值
对应的销售均价的估计值,3月份至7月份销售均价估计值![]() 与实际相应月份销售均价
与实际相应月份销售均价![]() 差的绝对值记为
差的绝对值记为![]() ,即
,即![]() ,
,![]() .若
.若![]() ,则将销售均价的数据
,则将销售均价的数据![]() 称为一个“好数据”,现从5个销售均价数据中任取
称为一个“好数据”,现从5个销售均价数据中任取
参考公式:回归方程系数公式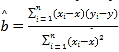 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
【题目】某市对全市高二学生的期末数学测试成绩统计显示,全市10000名学生的数学成绩服从正态分布![]() .现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
.现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
注:表中试卷编![]() .
.
(1)写出表中试卷得分为144分的试卷编号(写出具体数据即可);
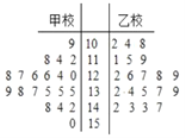
(2)该市又用系统抽样的方法从乙校中抽取了20份试卷,将甲乙两校这40份试卷的得分制作成如图所示的茎叶图,在这40份试卷中,从成绩在140分以上(含140分)的学生中任意抽取3人,这3人中数学成绩在全市排名前15名的人数记为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]()