2.设函数f(x)=x3-6x2+16x-5-sinπx,{an}是公差不为零的等差数列,若$\sum_{i=1}^{10}$f(ai)=110,则$\sum_{i=1}^{10}$ai=( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
17.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为$\sqrt{3}$,则四面体ABCD外接球的表面积为( )
| A. | 6π | B. | 7π | C. | 8π | D. | $\frac{{7\sqrt{7}}}{6}π$ |
15.某数学老师身高179cm,他爷爷、父亲和儿子的身高分别是176cm、173cm和185cm,因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测孙子的身高,已知父亲与儿子身高如表一:
该数学老师提供了三种求回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的方案(每种方案都正确).$\stackrel{∧}{b}$=$\frac{\sum_{\;}^{\;}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{\;}^{\;}{x}_{i}^{2}-{n\overline{x}}^{2}}$(公式1),$\stackrel{∧}{b}$=$\frac{\sum_{\;}^{\;}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{\;}^{\;}(x{{\;}_{i}-\overline{x}}^{2})}$(公式2);$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$(公式3)
(方案一):借助(公式1)求$\stackrel{∧}{b}$,借助(公式3),求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案二):借助(公式2)求$\stackrel{∧}{b}$,借助(公式3)求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案三):令X=x-173,Y=y-179,则(表一)转化成诶面的(表二).
借助(表二)和(公式1)、(公式3),求出$\stackrel{∧}{Y}$=$\stackrel{∧}{b}$X+$\stackrel{∧}{a}$,进而求出y对x的回归直线(y-179)=$\stackrel{∧}{b}$(x-173)+$\stackrel{∧}{a}$.
结合数据特点任选一种方案,求y与x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并根据回归直线预测数学教师的孙子的身高.
| 父亲身高x(cm) | 176 | 173 | 179 |
| 儿子身高y(cm) | 173 | 179 | 185 |
(方案一):借助(公式1)求$\stackrel{∧}{b}$,借助(公式3),求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案二):借助(公式2)求$\stackrel{∧}{b}$,借助(公式3)求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案三):令X=x-173,Y=y-179,则(表一)转化成诶面的(表二).
| X | 3 | 0 | 6 |
| Y | -6 | 0 | 6 |
结合数据特点任选一种方案,求y与x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并根据回归直线预测数学教师的孙子的身高.
14.为了研究“教学方式”对教学质量的影响,某高中英语老师分别用两种不同的教学方法对入学英语平均分和优秀率都相同的甲乙两个高一新班进行教学(勤奋程度和自觉性相同),以下茎叶图为甲乙两班(每班均20人)学生的英语期末成绩,若成绩不低于125分的为优秀,填写下面的2×2列联表,并判断是否有97.5%的把握认为“成绩优秀与教学方式有关”.
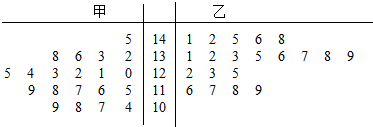
参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{{n}_{+2}}^{\;}}$
附表:
0 252685 252693 252699 252703 252709 252711 252715 252721 252723 252729 252735 252739 252741 252745 252751 252753 252759 252763 252765 252769 252771 252775 252777 252779 252780 252781 252783 252784 252785 252787 252789 252793 252795 252799 252801 252805 252811 252813 252819 252823 252825 252829 252835 252841 252843 252849 252853 252855 252861 252865 252871 252879 266669

| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
附表:
| P(X2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
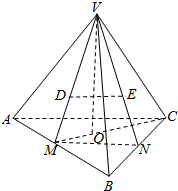 如图所示,已知D,E分别是三棱锥V-ABC的两个侧面VAB,VBC的重心.
如图所示,已知D,E分别是三棱锥V-ABC的两个侧面VAB,VBC的重心.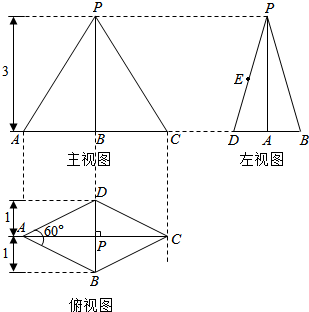 一个四棱锥的三视图和直观图如图所示,E为侧棱PD的中点.
一个四棱锥的三视图和直观图如图所示,E为侧棱PD的中点.