17.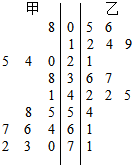 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间
各自的点击量,得到如图所示的统计图,根据统计图,甲、乙二者的中位数中较大那个为( )
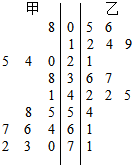 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间各自的点击量,得到如图所示的统计图,根据统计图,甲、乙二者的中位数中较大那个为( )
| A. | 55 | B. | 56.5 | C. | 37 | D. | 36.5 |
16.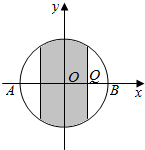 如图所示,在单位圆O的某一直径AB上随机地取一点Q,则过点Q且与该直径垂直的
如图所示,在单位圆O的某一直径AB上随机地取一点Q,则过点Q且与该直径垂直的
弦的长度不超过1的概率( )
 如图所示,在单位圆O的某一直径AB上随机地取一点Q,则过点Q且与该直径垂直的
如图所示,在单位圆O的某一直径AB上随机地取一点Q,则过点Q且与该直径垂直的弦的长度不超过1的概率( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | 1-$\frac{\sqrt{2}}{2}$ |
15.盒子里有3个红球,2个白球,现从中任取二个球,设事件M={2个球都是白球}.事件N={2个球中有1红球,1白球},事件P={2个球都是红球},事件Q={2个球中至少有1个红球},则满足对立事件的为( )
| A. | M与N | B. | N与P | C. | M与Q | D. | N与Q |
14.已知圆x2+y2-2x+4y+1=0,则原点O在( )
| A. | 圆内 | B. | 圆外 | C. | 圆上 | D. | 无法判断 |
13.点P(-1,2,3)关于zOx平面对称的点的坐标是( )
| A. | (1,2,3) | B. | (-1,-2,3) | C. | (-1,2,-3) | D. | (1,-2,-3) |
12.为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组数如下:
[10.75,10.85)3;[10.85,10.95)9;[10.95,11.05)13;
[11.05,11.15)16;[11.15,11.25)26;[11.25,11.35)20;
[11.35,11.45)7;[11.45,11.55)4;[11.55,11.65)2;
估计数据落在[10.95,11.35)范围内的频率为( )
[10.75,10.85)3;[10.85,10.95)9;[10.95,11.05)13;
[11.05,11.15)16;[11.15,11.25)26;[11.25,11.35)20;
[11.35,11.45)7;[11.45,11.55)4;[11.55,11.65)2;
估计数据落在[10.95,11.35)范围内的频率为( )
| A. | .035 | B. | 0.5 | C. | 0.75 | D. | 0.95 |
11.x2+(y+2)2=3的圆心坐标、半径分别为( )
0 252434 252442 252448 252452 252458 252460 252464 252470 252472 252478 252484 252488 252490 252494 252500 252502 252508 252512 252514 252518 252520 252524 252526 252528 252529 252530 252532 252533 252534 252536 252538 252542 252544 252548 252550 252554 252560 252562 252568 252572 252574 252578 252584 252590 252592 252598 252602 252604 252610 252614 252620 252628 266669
| A. | (0,2);3 | B. | (0,-2);3 | C. | $({0,2});\sqrt{3}$ | D. | $({0,-2});\sqrt{3}$ |
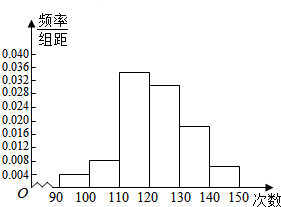 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.则 样本容量为150.
为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.则 样本容量为150.