15.某顾客购车后,从(X,Y,Z,T)中选两个不同的字母,从{0,2,6,8}中选3个不同的数字作为车牌号,要求前3位是数字,后2位是字母,且数字2不能排在首位,字母Z和数字2不能相邻,若该顾客选择的车牌号中含有字母Z和数字2,则可供选择的车牌号的各位为( )
| A. | 36 | B. | 54 | C. | 72 | D. | 162 |
12.若极坐标方程ρ=ρ(θ)满足ρ(θ)=ρ(π-θ),则方程ρ=ρ(θ)表示的图形关于( )
| A. | 极轴对称 | B. | 极点对称 | C. | 射线θ=$\frac{π}{2}$对称 | D. | 不能确定 |
10.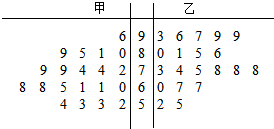 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,吴老师采用A,B两种不同的数学方式对甲、乙两个班进行教学实验,为了解教学效果,期末考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下:(记成绩不低于90分者为“成绩优秀”).
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,吴老师采用A,B两种不同的数学方式对甲、乙两个班进行教学实验,为了解教学效果,期末考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下:(记成绩不低于90分者为“成绩优秀”).
(1Ⅰ)在乙班样本的20个个体中,从不低于80分的成绩中不放回地抽取2次,每次抽取1个,求在第1次抽取的成绩低于90分的前提下,第2次抽取的成绩仍低于90分的概率;
(Ⅱ)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.1的前提下认为“成绩优秀”与数学方式有关?
独立性检验临界值表:
 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,吴老师采用A,B两种不同的数学方式对甲、乙两个班进行教学实验,为了解教学效果,期末考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下:(记成绩不低于90分者为“成绩优秀”).
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,吴老师采用A,B两种不同的数学方式对甲、乙两个班进行教学实验,为了解教学效果,期末考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下:(记成绩不低于90分者为“成绩优秀”).(1Ⅰ)在乙班样本的20个个体中,从不低于80分的成绩中不放回地抽取2次,每次抽取1个,求在第1次抽取的成绩低于90分的前提下,第2次抽取的成绩仍低于90分的概率;
(Ⅱ)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.1的前提下认为“成绩优秀”与数学方式有关?
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 01010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.027 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样方法在校园内调查了120位学生,得到如下2×2列联表:
则a-b-c等于( )
0 249268 249276 249282 249286 249292 249294 249298 249304 249306 249312 249318 249322 249324 249328 249334 249336 249342 249346 249348 249352 249354 249358 249360 249362 249363 249364 249366 249367 249368 249370 249372 249376 249378 249382 249384 249388 249394 249396 249402 249406 249408 249412 249418 249424 249426 249432 249436 249438 249444 249448 249454 249462 266669
| 男 | 女 | 总计 | |
| 爱好 | a | b | 73 |
| 不爱好 | c | 25 | |
| 总计 | 74 |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
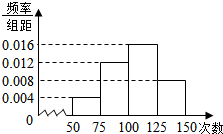 为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.
为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.