题目内容
(本题满分14分)
已知函数f(x)=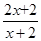 ,若数列
,若数列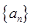 ,
,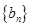 满足
满足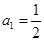 ,
,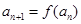 ,
,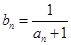
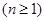 ,
,
(1)求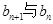 的关系,并求数列
的关系,并求数列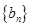 的通项公式;
的通项公式;
(2)记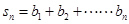 , 若
, 若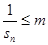 恒成立.求
恒成立.求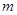 的最小值.
的最小值.
(1) bn= (
(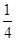 )n-1+
)n-1+ .(2) m的最小值为
.(2) m的最小值为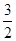 。
。
解析试题分析:(1)根据递推关系和已知的所求解的,构造那个结构特点的关系式,进而得到结论。(2)利用第一问的结论得到数列{bn- }是首项b1-
}是首项b1- =
= ,公比为
,公比为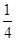 的等比数列,进而得到通项公式,并求解和式。
的等比数列,进而得到通项公式,并求解和式。
解:(1)∵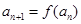 ,∴
,∴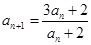 .………2
.………2
又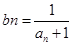 ,∴
,∴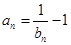 ,
, .………3
.………3
∴代入化简得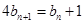 ,………4 ∴
,………4 ∴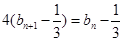
∴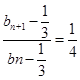 ,………6∴数列{bn-
,………6∴数列{bn- }是首项b1-
}是首项b1- =
= ,公比为
,公比为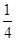 的等比数列,
的等比数列,
∴bn- =
= (
(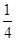 )n-1,bn=
)n-1,bn= (
(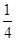 )n-1+
)n-1+ .………………8
.………………8
(2)Sn=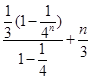 =
=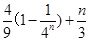 …10
…10
∴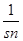 =
=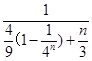 ≤
≤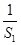 =
=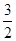 ,………12∴
,………12∴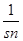 的最大值为
的最大值为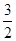 ,又
,又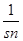 ≤m,
≤m,
∴m的最小值为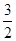 ………………………14
………………………14
考点:本试题主要考查了数列通项公式和前n项和的求解的综合运用。
点评:解决该试题的关键是对于分式递推式,采用取倒数的方法得到递推关系式,并能结合分组求和的思想得到数列的 前n项和问题。

练习册系列答案
相关题目
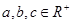 ,设
,设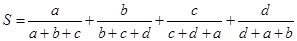 ,则下列判断中正确的是( )
,则下列判断中正确的是( )
A.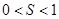 | B.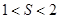 | C.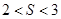 | D. |
 是等比数列,
是等比数列,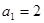 ,且
,且 是
是 的等差中项.
的等差中项.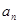 ;
;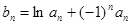 ,求数列
,求数列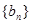 的前n项和
的前n项和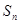 .
.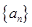 是等差数列,数列
是等差数列,数列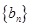 是等比数列,且对任意的
是等比数列,且对任意的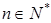 ,都有
,都有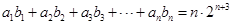 .
.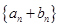 的前
的前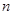 项和
项和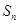 ;
;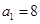 .
.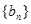 中是否存在某一项,它可以表示为该数列中其它
中是否存在某一项,它可以表示为该数列中其它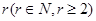 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由.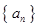 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,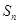 为其前n项和,且满足
为其前n项和,且满足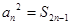 ,
,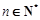 .数列
.数列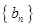 满足
满足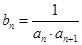 ,
, 为数列
为数列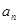 和数列
和数列 ,不等式
,不等式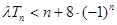 恒成立,求实数
恒成立,求实数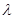 的取值范围;
的取值范围;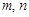
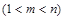 ,使得
,使得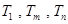 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有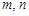 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.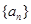 ,前
,前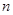 项和为
项和为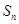 .且满足
.且满足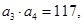
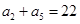 .
.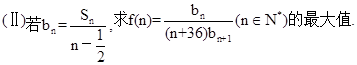
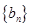 中,
中,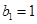 ,且点
,且点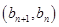 在直线
在直线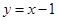 上.数列
上.数列 中,
中,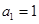 ,
, ,
, ,求数列
,求数列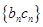 的前
的前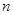 项和
项和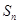 .
.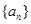 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列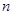 项和。
项和。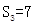 ,且
,且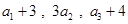 构成等差数列.
构成等差数列.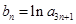 ,求数列
,求数列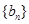 的前
的前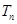 .
.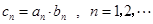 ,求数列
,求数列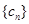 的前
的前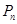 .
.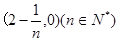 且方向向量为
且方向向量为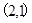 的直线交椭圆
的直线交椭圆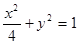 于
于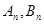 两点,记原点为
两点,记原点为 ,
,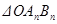 面积为
面积为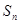 ,则
,则 _______
_______