题目内容
集合P=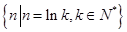 ,若
,若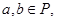 则
则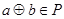 ,那么运算
,那么运算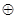 可能是( )
可能是( )
| A.加法 | B.减法 | C.乘法 | D.除法 |
A
解析考点:元素与集合关系的判断.
专题:新定义.
分析:由已知中集合P={n|n=lnk,k∈N*},根据集合元素与集合关系的定义,我们可得当a,b∈P时,存在A,B∈N*使a=lnA,b=lnB,进而根据对数的运算法则,判断出当运算⊕为加法时,满足条件.
解答:解:∵集合P={n|n=lnk,k∈N*},
若a,b∈P,则
存在A,B∈N*使a=lnA,b=lnB
则a+b=lnA+lnB=ln(AB),
∵A?B∈N*,
∴a+b∈P成立,
故选A
点评:本题考查的知识点是元素与集合的判断,对数的运算性质,其中正确理解元素与集合的关系的概论,是解答本题的关键.

练习册系列答案
相关题目
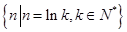 ,若
,若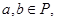 则
则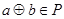 ,那么运算
,那么运算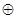 可能是(
)
可能是(
)