Question

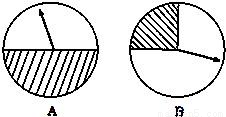
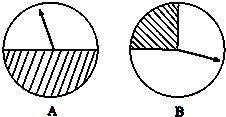如图，两个圆形转盘A，B，每个转盘阴影部分各占转盘面积的

1

2

和

1

4

．某“幸运转盘积分活动”规定，当指针指到A，B转盘阴影部分时，分别赢得积分1000分和2000分．先转哪个转盘由参与者选择，若第一次赢得积分，可继续转另一个转盘，此时活动结束；若第一次未赢得积分，则终止活动．
（Ⅰ）记先转A转盘最终所得积分为随机变量X，则X的取值分别是多少？
（Ⅱ）如果你参加此活动，为了赢得更多的积分，你将选择先转哪个转盘？请说明理由．

Answer 1

分析：（1）先转转盘A未转到阴影部分则得到0分，转到阴影部分得到1000分，还可以继续转B盘，若B盘转不到阴影部分只得1000分，若B盘转到阴影部分则可以得到3000分，得到变量的取值．
（2）由已知得，转动A盘得到积分的概率为

1

2

，转动B盘得到积分的概率为

1

4

．两个转盘转动是相互独立的，根据相互独立事件同时发生的概率做出两个变量的得分期望，进行比较得到结果．

解答：解：（Ⅰ）先转A转盘最终所得积分为随机变量X，
先转转盘A未转到阴影部分则得到0分，转到阴影部分得到1000分，还可以继续转B盘，
若B盘转不到阴影部分只得1000分，若B盘转到阴影部分则可以得到3000分，
X的取值分别是：0分，1000分，3000分．
（Ⅱ）由已知得，转动A盘得到积分的概率为

1

2

，转动B盘得到积分的概率为

1

4

．
设先转A盘所得的积分为X分，先转B盘所得的积分为Y分．
则有P(X=0)=1-

1

2

=

1

2

，
P(X=1000)=

1

2

×(1-

1

4

)=

3

8

，
P(X=3000)=

1

2

×

1

4

=

1

8

．
∴EX=0×

1

2

+1000×

3

8

+3000×

1

8

=

6000

8

．
同理P(Y=0)=

3

4

，
P(Y=2000)=

1

8

，
P(Y=3000)=

1

8

．
∴EY=0×

3

4

+2000×

1

8

+3000×

1

8

=

5000

8

．
故先转A盘时，赢得积分平均水平较高．

点评：期望是概率论和数理统计的重要概念之一，是反映随机变量取值分布的特征数，学习期望将为今后学习概率统计知识做铺垫，它在市场预测，经济统计，风险与决策等领域有着广泛的应用，为今后学习数学及相关学科产生深远的影响．