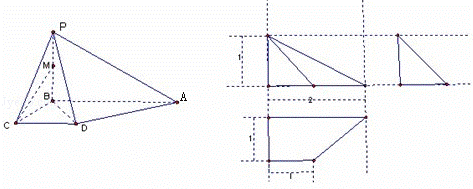
题目内容
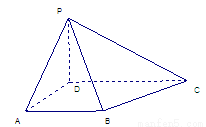
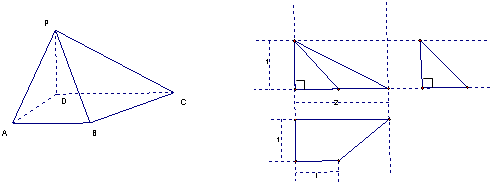 一个四棱锥的直观图和三视图如图所示:
一个四棱锥的直观图和三视图如图所示:(1)求证:BC⊥PB;
(2)求出这个几何体的体积.
(3)若在PC上有一点E,满足CE:EP=2:1,求证PA∥平面BED.
分析:(1)由三视图可知:PD⊥底面ABCD,底面ABCD为直角梯形,AB=AD=1,CD=2.由条件利用直线和平面垂直的判定定理证明BC⊥平面PBD,从而证明BC⊥PB.
(2)由题意可得PD是这个四棱锥的高,求得底面SABCD=
×(AB+CD)×AD的值,再由 VP-ABCD=
×SABCD×PD,运算求得结果.
(3)设AC交BD于O点,可得
=
=
,再由
=
,可得
=
=
,从而PA∥EO,由此可得PA∥平面BED.
(2)由题意可得PD是这个四棱锥的高,求得底面SABCD=
| 1 |
| 2 |
| 1 |
| 3 |
(3)设AC交BD于O点,可得
| CD |
| AB |
| CO |
| AO |
| 2 |
| 1 |
| CE |
| EP |
| 2 |
| 1 |
| CO |
| AO |
| CE |
| EP |
| 2 |
| 1 |
解答:解:(1)由三视图可知:PD⊥底面ABCD,底面ABCD为直角梯形,AB=AD=1,CD=2.
∵PD⊥底面ABCD,BC?平面ABCD,∴PD⊥BC.…(1分)
在梯形ABCD中,PD=AD=AB=1,CD=2,∴BD=
,又可得BC=
,CD=2,∴DB⊥BC.…(2分)
又∵PD∩BD=D,BD,PD?平面PBD,∴BC⊥平面PBD.
再由PB?平面PBD,∴BC⊥PB.…(5分)
(2)∵PD⊥平面ABCD,∴PD是这个四棱锥的高,…(6分)
∵底面SABCD=
×(AB+CD)×AD=
×(2+4)×2=6,…(7分)
∴VP-ABCD=
×SABCD×PD=
×6×2=4…(8分)
(3)连结AC,设AC交BD于O点,∵CD∥AB,CD=2AB,∴
=
=
.(10分)
又∵
=
,∴
=
=
(,12分)∴PA∥EO.
EO?平面BED,PA?平面BE,∴PA∥平面BED…(14分)
∵PD⊥底面ABCD,BC?平面ABCD,∴PD⊥BC.…(1分)
在梯形ABCD中,PD=AD=AB=1,CD=2,∴BD=
| 2 |
| 2 |
又∵PD∩BD=D,BD,PD?平面PBD,∴BC⊥平面PBD.
再由PB?平面PBD,∴BC⊥PB.…(5分)
(2)∵PD⊥平面ABCD,∴PD是这个四棱锥的高,…(6分)
∵底面SABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
(3)连结AC,设AC交BD于O点,∵CD∥AB,CD=2AB,∴
| CD |
| AB |
| CO |
| AO |
| 2 |
| 1 |
又∵
| CE |
| EP |
| 2 |
| 1 |
| CO |
| AO |
| CE |
| EP |
| 2 |
| 1 |
EO?平面BED,PA?平面BE,∴PA∥平面BED…(14分)
点评:本题主要考查直线和平面垂直的判定定理、性质定理的应用,直线和平面平行的判定定理的应用,求棱锥的体积,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
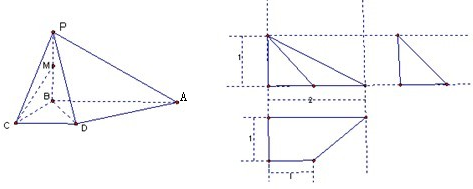 一个四棱锥的直观图和三视图如图所示:
一个四棱锥的直观图和三视图如图所示: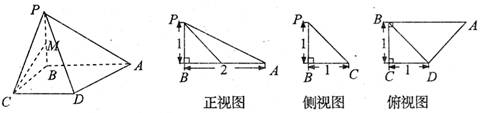

 ⊥
⊥ ;
;